Algo de teoría sobre las ondas

Vibraciones y Ondas

Las vibraciones y ondas están muy presentes en todos los aspectos de nuestra vida, desde el movimiento que realizamos para bailar el hula hoop, hasta los mecanismos de percepción que hemos desarrollado en torno a la vibración, como son la vista y el oído (Crowell, 2000). Las ondas de luz, que nos permiten ver y percibir colores, implican vibración. Podemos escuchar y hablar porque nuestros tímpanos y cuerdas vocales vibran, nuestros corazones laten de manera periódica y nuestros pulmones inhalan y exhalan aire repetidamente.  (French, 1971). 

Figura.1 Niñx vibrando con un aro. 

Las Vibraciones son movimientos que se repiten una y otra vez en torno a una posición de equilibrio ("Vibración", 2022), un movimiento repetitivo que también se conoce como movimiento oscilatorio (French, 1971). 

                     

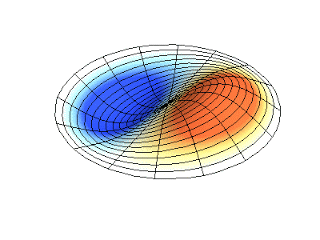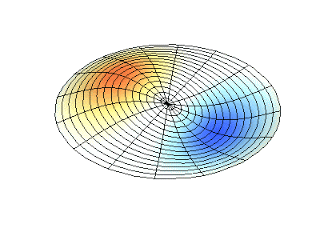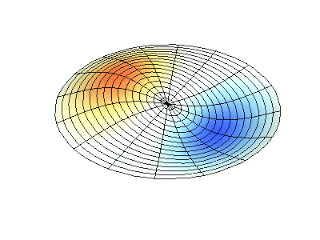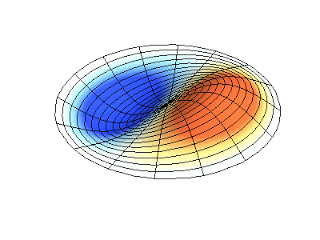
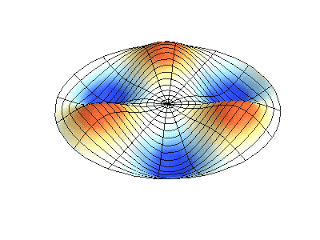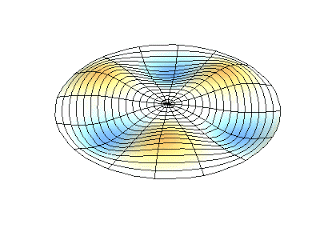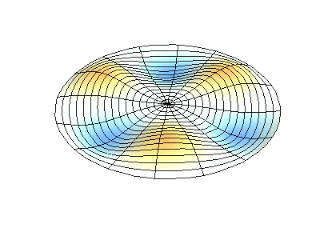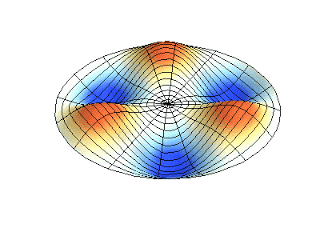
Figura 2. Representación de dos modos de vibración periódica

Periodo, frecuencia y amplitud

Un movimiento que se repite una y otra vez se conoce como movimiento periódico, y el tiempo necesario para llevar a cabo una repetición se denomina periodo, T.  El número de repeticiones por segundo es la frecuencia, f (Crowell, 2000). La frecuencia y el periodo son magnitudes que dependen de la fuente que origina la vibración.

f = 1/T

Como podéis observar la frecuencia (f) es la inversa del periodo (T). Luego T y f son dos unidades que permiten medir la relación entre tiempo y repetición de movimientos oscilatorios. El periodo se mide en segundos, y la frecuencia en Hercios, Hz.

Figura 3. Persona bailando el hula hoop 

Por ejemplo, una persona bailando un aro alrededor de su cintura, realiza un movimiento periódico, un movimiento que se repite. Vamos a fijarnos ahora en el aro, cada vez que el aro toca su ombligo contaremos una vuelta o una repetición. El tiempo que tarda el aro en volver a pasar por el ombligo sera el periodo (T), y la frecuencia (f) es cuantas veces por segundo pasa el aro por el ombligo. Podemos intuir que la velocidad con la que el aro gira va a estar relacionada con el periodo (T) y la frecuencia (f), cuanto más rápido gire el aro menor sera el tiempo que tarda en pasar por el ombligo, luego menor sera el periodo (T). Sin embargo, cuanto más rápido gire el aro, mayor sera la frecuencia (f), ya que el aro pasará más veces por el ombligo, en el mismo periodo de tiempo. 

El tamaño de las vibraciones se refleja en la amplitud A, que se relaciona con el valor máximo alcanzado en cada repetición y se define en física de forma general, como la distancia desde el centro a uno de los extremos del movimiento (Crowell, 2000). Las unidades de la amplitud dependerán de la escala y tipo de movimiento.

Figura 4. Amplitud del movimiento del aro en una persona bailando un hula hoop.

Cualquier vibración contiene energía, y el valor de esa energía es proporcional a la amplitud. Sin embargo, el periodo y la frecuencia son independientes de la amplitud (Crowell, 2000).

¿Qué son las ondas? 

Figura 5. Niñx vibrando. La vibración no se transmite al aro.

En la imagen superior vemos como la niña vibra, pero no consigue que el movimiento de su vibración se traslade al aro, que cae inmóvil al suelo mientras el niño continúa vibrando. La intención de la niña es la de mover el aro con su vibración, transmitir el movimiento que realiza con su cuerpo a otro objeto, pero, no lo consigue. Por otro lado, en la figura 2, la persona sí logra transmitir el movimiento de su cuerpo al aro que se mueve alrededor de ella de manera periódica.

Una vez tenemos claro qué es una vibración, es el momento de pasar a hablar sobre las ondas. Estas se producen como consecuencia de oscilaciones y vibraciones de la materia ("Onda", 2021). En física, una onda (del latín unda) consiste en la propagación de una perturbación de alguna propiedad del espacio, por ejemplo, densidad, presión, campo eléctrico o campo magnético, implicando un transporte de energía sin transporte de materia. ("Onda", 2022). 

Figura 6. Fila de personas cayendo por el empuje de la última.

Para entenderlo mejor, vamos a utilizar una metáfora que si queréis podéis utilizar para explicárselo a vuestros alumnos. Imagina que tenemos una fila de 5 niños esperando para entrar en clase. El ultimo niño, al que asignaremos la posición 5, empuja al que tiene delante: niño número 4. El niño 4 sin poder evitarlo se precipita sobre el 3, que a su vez se precipita sobre el 2 que inevitablemente empuja al 1, que choca contra la puerta. Sin que los niños se desplacen, el empujón del niño 5 ha llegado hasta la puerta, lo mismo sucede con las ondas, sin que la materia se desplace, una perturbación se propaga a través del espacio.
Este movimiento, iniciado por el niño 5, se ha transmitido de niño en niño en una reacción en cadena, como en el ejemplo clásico de la fila de fichas de dominó cayendo. La perturbación en la fila causada por el niño 5 ha llegado hasta la puerta pasando de niño en niño. Vemos, por tanto, que la fila es el medio y que los niños son las partículas del medio. 

Las magnitudes que hemos visto relacionadas con las vibraciones: periodo (T), frecuencia (f) y aptitud (A); se aplican también a las ondas. 

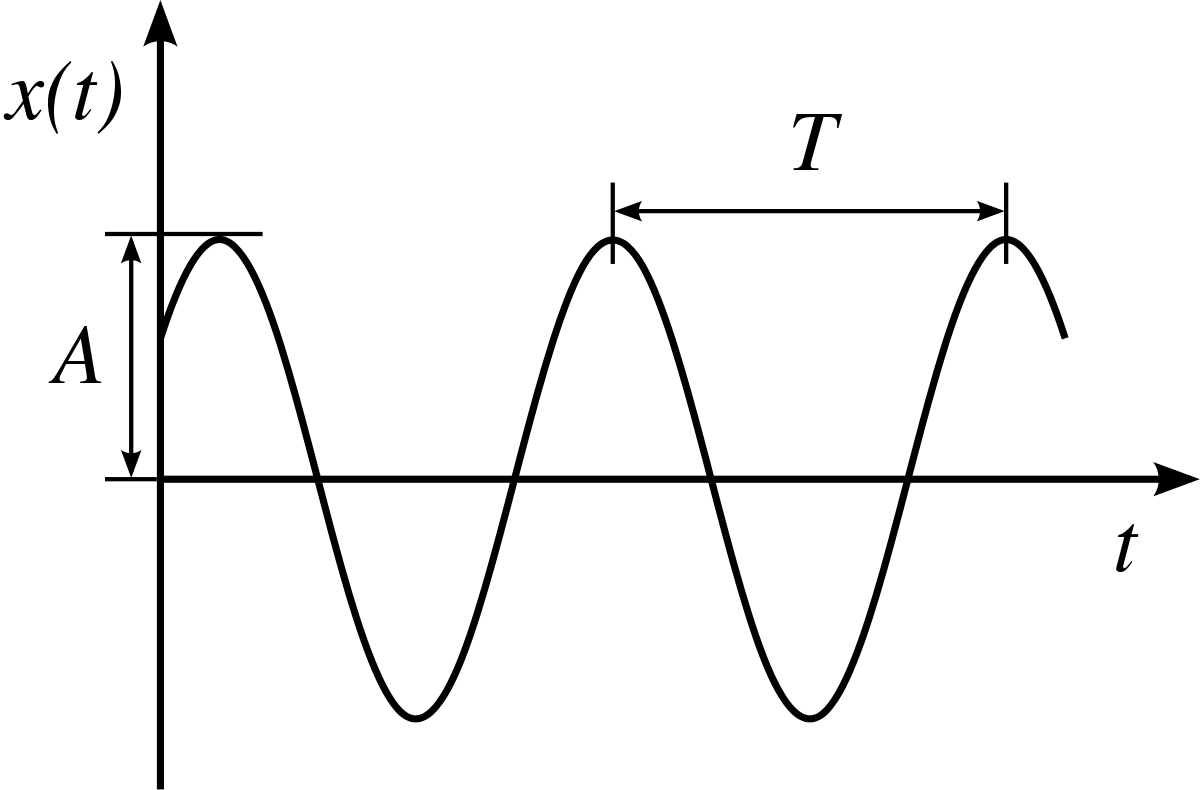
Figura 7. Amplitud (A) y periodo (T) en una onda representada en función del tiempo.

Las ondas y su clasificación

Las propiedades físicas de las ondas dependen y varían en función del origen y medio a través del cual se propagan (Onda, 2021). Las clasificamos de la siguiente manera:

1. Según el MEDIO en que se propagan:

• Ondas MECÁNICAS. Precisan de un medio elástico (líquido, gaseoso o sólido) y de condiciones determinadas de temperatura y presión, para propagarse efectivamente. Por ejemplo: las ondas sonoras que se propagan por el aire o por el agua y que veremos en el proximo capitulo.
• Ondas ELECTROMAGNÉTICAS. No requieren de un medio porque se pueden propagar en el vacío. Por ejemplo: la luz. De la que volveremos a hablar en la página siguiente.
  
• Ondas GRAVITACIONALES. Alteraciones del espacio-tiempo (recién confirmadas por la ciencia).

2. Según su PERIODICIDAD:

• Ondas PERIÓDICAS. Presentan ciclos repetitivos o regulares.
• Ondas NO PERIÓDICAS. Presentan ciclos irregulares.

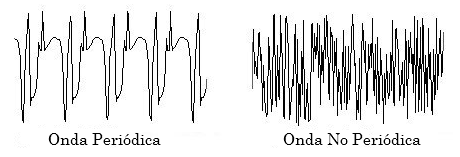Figura 8. Representación de una onda periódica (izquierda) y de una onda no periódica (derecha)

3. Según su DIRECCIÓN:

• Ondas UNIDIMENSIONALES. Se propagan a través de una sola dimensión en el espacio. 

          Figura 9. Onda unidimensional.

• Ondas BIDIMENSIONALES. Se propagan a través de dos dimensiones y se suelen llamar también superficiales. 

    Figura 10. Onda bidimensional.

• Ondas TRIDIMENSIONALES. Se propagan en tres dimensiones y suelen llamarse esféricas.

Figura 11. Onda tridimensional.

Según el MOVIMIENTO DEL MEDIO respecto a la dirección en que se propague la onda:

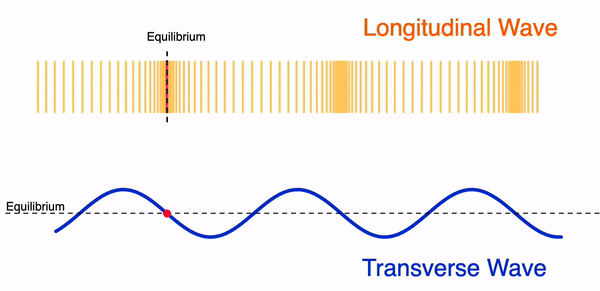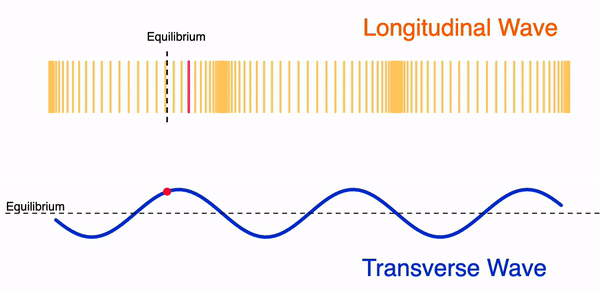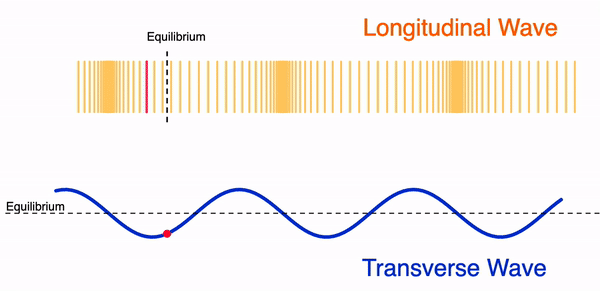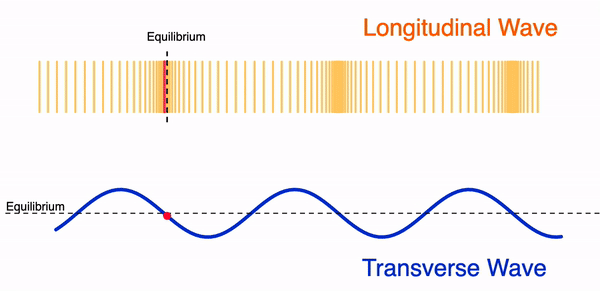
• Ondas LONGITUDINALES. Las partículas del medio se mueven en la misma dirección en que se propaga la onda.
• Ondas TRANSVERSALES. Las partículas vibran perpendicularmente a la dirección de propagación de la onda.
  

  
  

Figura 12. Movimiento de una onda longitudinal (arriba) y de una onda transversal (abajo). La marca roja en ambos casos indica una partícula del medio y como esta se mueve.

Aquí tienes algunos ejemplos de tipos de ondas:

• Sonido de una flauta tocando la nota Do: Onda mecánica, periódica, tridimensional y longitudinal.
• Sonido ruido blanco: Onda mecánica, no periódica, tridimensional y longitudinal.
• Perturbación de una gota en el agua que cae en un lago: Onda mecánica, periódica, bidimensional y transversal.
• La luz visible: Onda electromagnética, periódica, tridimensional y transversal.

Partes de una onda.

En la siguiente imagen vemos las partes de una onda que se propaga en el espacio: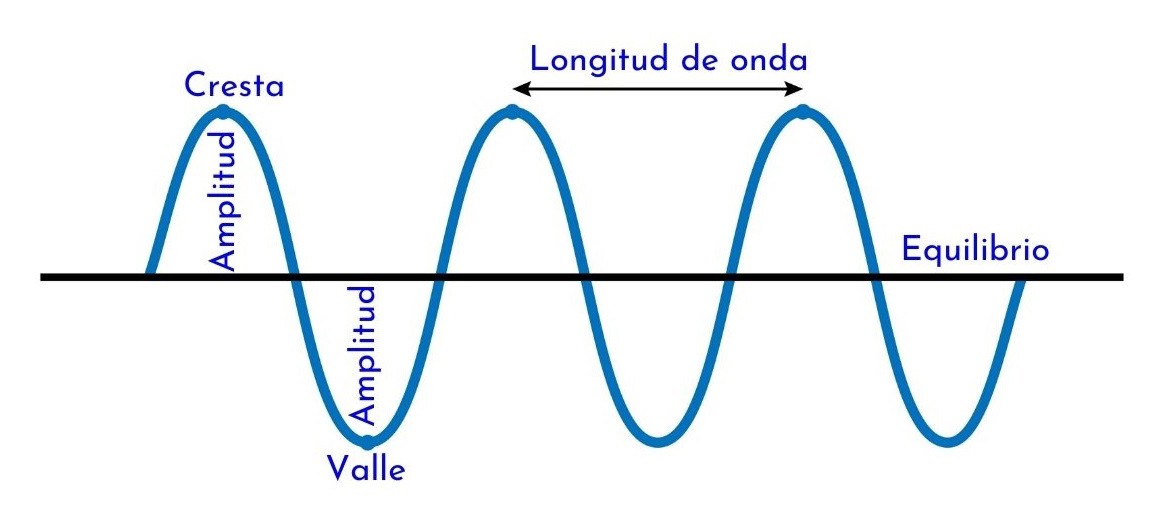

Figura 13. Partes de una onda: Cresta, valle, amplitud (A), longitud de onda (λ) y el eje de equilibrio.

Longitud de onda

La longitud de onda, representada por la letra λ, hace referencia al espacio que avanza el movimiento en cada repetición, y se puede definir como el espacio que abarca cada una de esas repeticiones. Para medirla tomaremos como punto de referencia una cresta, por lo tanto, la longitud de onda sera la distancia entre dos crestas consecutivas. Debemos tener cuidado, porque la longitud de onda guarda ciertas similitudes con el periodo. Ambas nos hablan de la repetición del movimiento, pero existe una diferencia fudnamental entre ambas, ya que la longitud de onda (λ) registra espacio, y el periodo (T) registra tiempo. Cuando veamos gráficas debemos tener en cuenta el sistema de representación que se utiliza, y fijarnos no solo en qué variables representan los ejes vertical y horizontal, sino también en qué unidades se presentan estas variables.

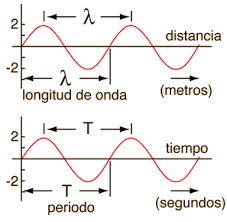Figura 14. Representación de una onda en función del espacio (arriba) y una onda en función del tiempo (abajo)

En la figura 14, el eje horizontal del gráfico superior representa el espacio, por eso, la magnitud entre crestas medida en metros, es la longitud de onda (λ). En el gráfico inferior, el eje horizontal representa el tiempo, por lo que la magnitud definida por la distancia entre crestas es el periodo (T) y se mide en segundos.
Debemos fijarnos en que aunque en esta imagen la longitud de onda y el periodo se representen de forma equivalente, sus valores no lo son. T y λ son variables diferentes y relacionándolas podemos obtener la velocidad de la onda (v), ya que la velocidad es el espacio recorrido en un tiempo determinado.

v = λ / T = λ f

Sobre la velocidad volveremos a hablar más adelante cuando aparezcan los conceptos de reflexión y refracción.

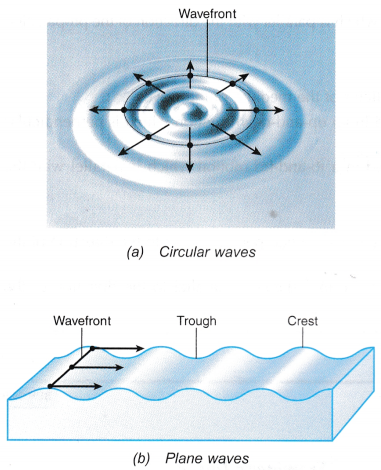
Frente de onda

El frente de onda es el lugar geométrico de los puntos del medio que se encuentran afectados por la perturbación en un instante determinado. Tomaremos las crestas como referencia, por lo que la distancia entre frentes de onda es igual a la longitud de onda. La dirección de propagación de un frente de onda es perpendicular al mismo.

Figura 15. Frente de onda en una onda circular(arriba) y en una onda plana (abajo).

Principio de Fresnel - Huygens

Este método plantea un modelo que nos va a permitir analizar y comprender cómo se propagan las ondas y nos sera útil para entender los fenómenos que con ellas ocurren. 

"Todo punto de un frente de onda inicial puede considerarse como una fuente de ondas esféricas secundarias que se extienden en todas las direcciones con la misma velocidad, frecuencia y longitud de onda que el frente de onda del que proceden." ("Principio de Fresnel", 2020)

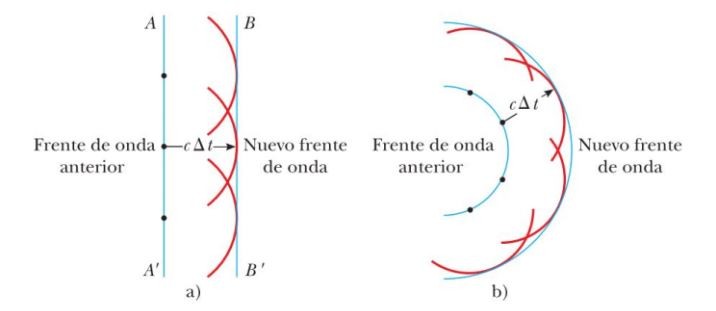Figura 16. Representación del principio de Fresnel-Huygens en una onda plana (izquierda) y en una onda circular (derecha)

Retomando nuestro ejemplo de la fila de niños, vemos como cada niño que recibe un empujón, genera a su vez otro empujón sobre el siguiente niño, en la misma dirección que el empujón recibido. Digamos que cada niño se convierte en un origen secundario de un nuevo empujón. 

Relación entre ondas

Superposición

Algo muy interesante sobre las ondas es que, a diferencia del movimiento de objetos, que al entrar en contacto generan fuerzas de repulsión entre ellos, las ondas se superponen en una misma región del espacio sin repulsión, y en el punto en el que coinciden se suman (Crowell, 2000. p.40).

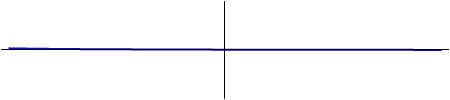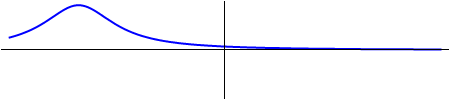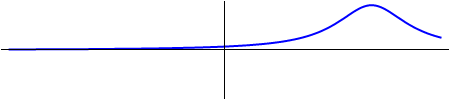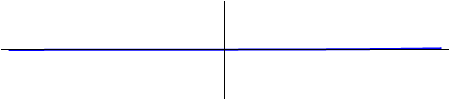Figura 17. Dos ondas con diferente dirección de desplazamiento.

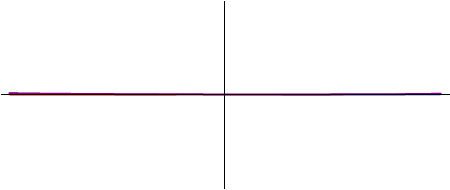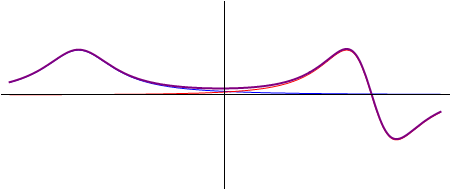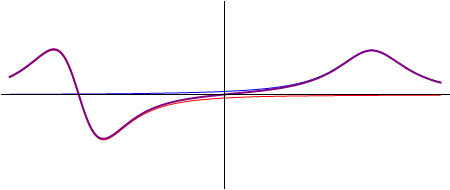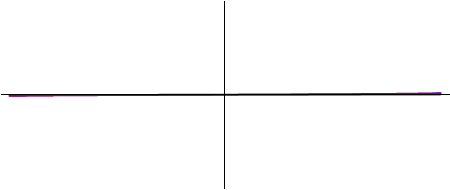Figura 18. Resultado de la superposición de las ondas de la figura 17.

Video 1.  Superposición de ondas superficiales en el agua.

Fase

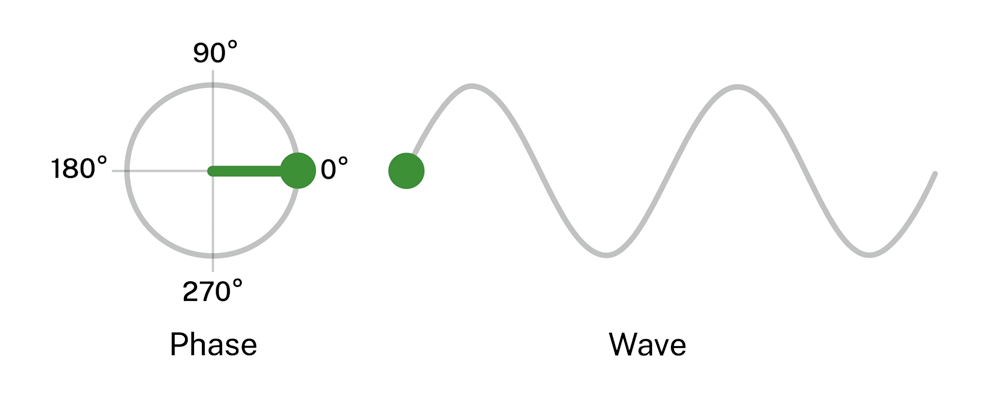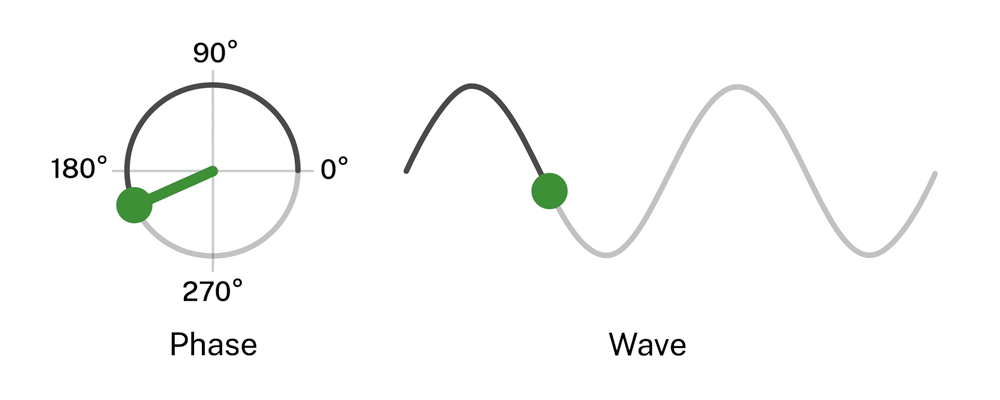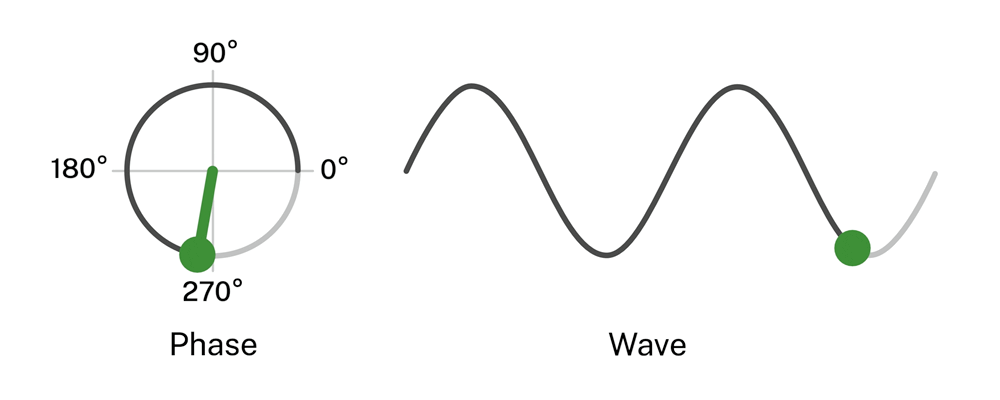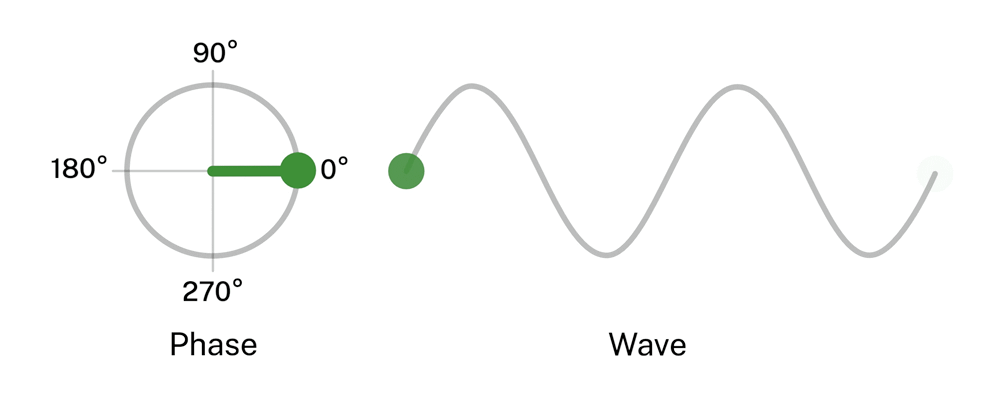
Otro concepto importante a la hora de trabajar con ondas, sobre todo lo podremos aplicar en el sonido, es el de la fase. La fase de una onda φ, es la posición relativa de un punto a lo largo de la onda (Polyakov, 2022). Es decir, en que posición de la repetición se encuentra un punto, en un momento determinado. La mediremos en función del ángulo descrito por su representación circular, en la que una repetición representa el circulo completo:

Figura 19. Representación de la fase de una onda. (Phase=fase, Wave=onda)

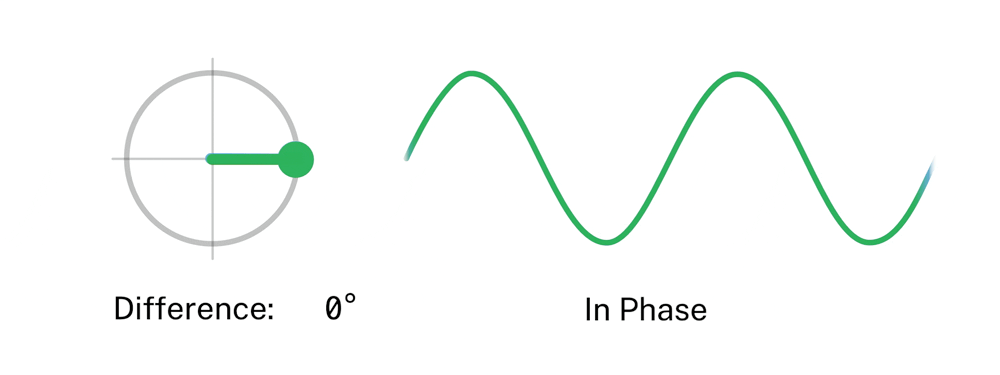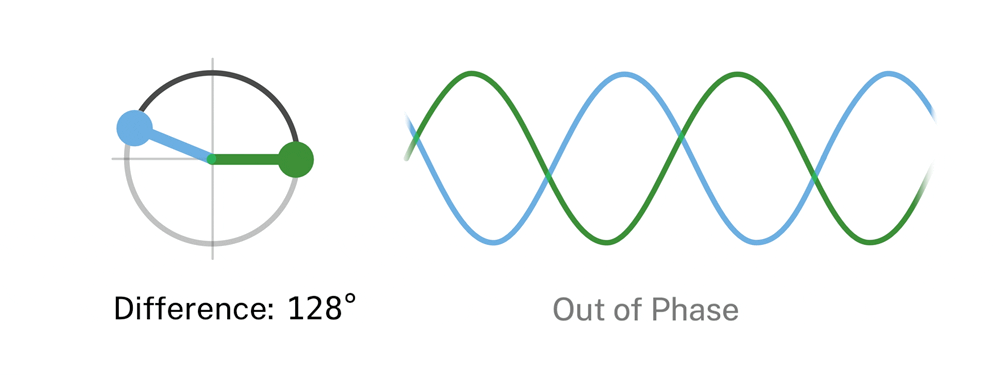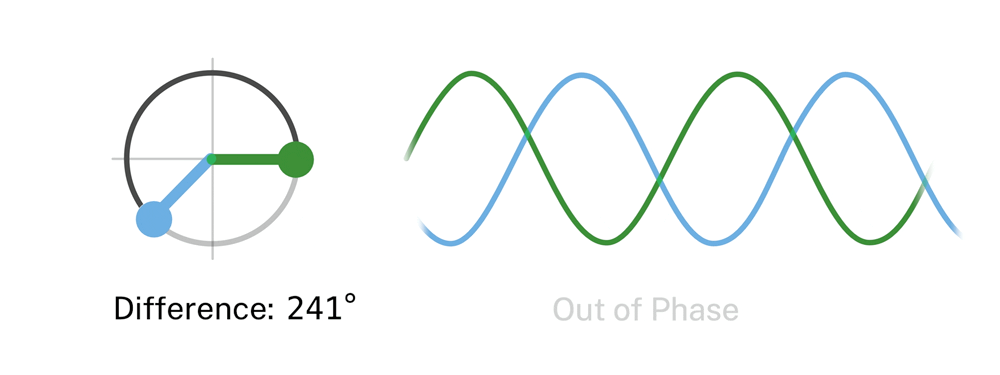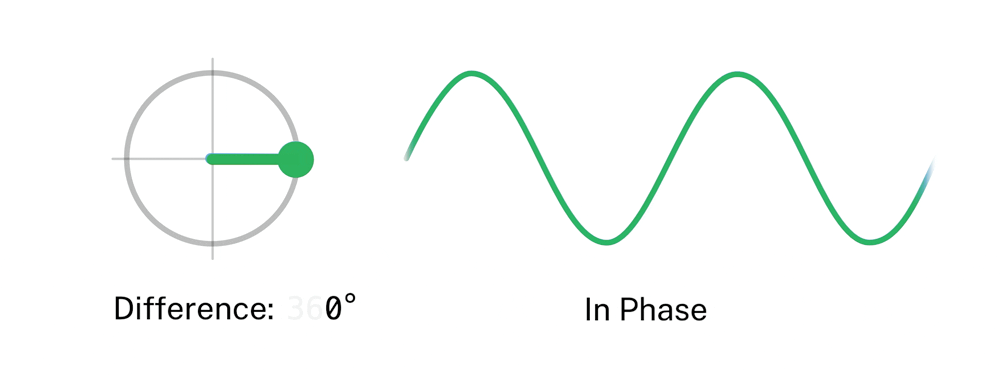
Esta magnitud cobra importancia al comparar las fases de varias ondas. A esta comparación la llamaremos diferencia de fase. Y la mediremos en grados o radianes. 

 

Figura 20. Representación de la diferencia de fase entre dos ondas con la misma frecuencia. (Phase=fase, Wave=onda)

La diferencia de fase va a influir en el resultado de la superposición de ondas. Podemos comprobar, que cuando la diferencia de fase es 180º las ondas se anulan, en este caso decimos que la fase de una, es la inversa de la otra y que se encuentran en oposición de fase. 

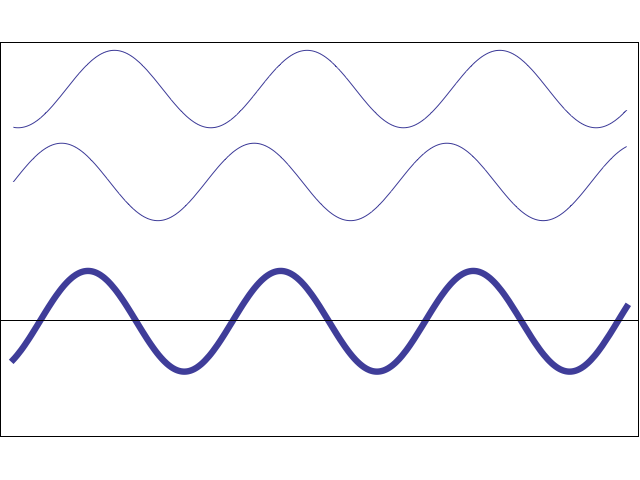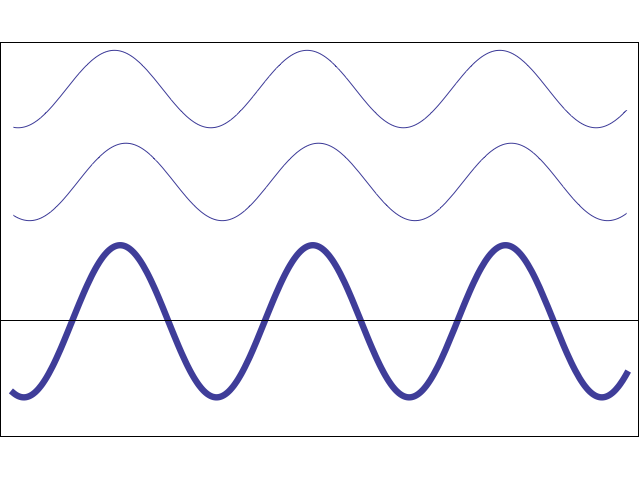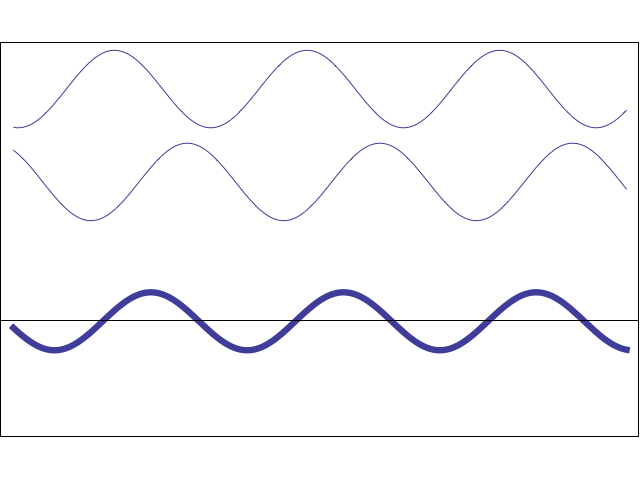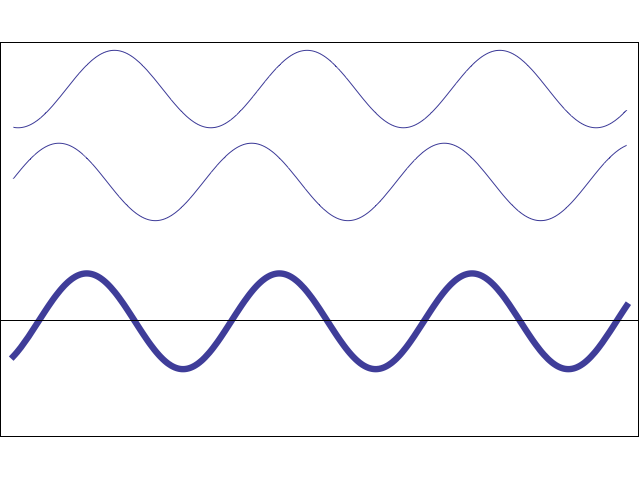Figura 21. Resultado de la suma de dos ondas sinusoidales de la misma frecuencia, pero diferencia de fase variable.

Para entenderlo un poco mejor vamos a volver al símil del hula hop pero con 2 aros en lugar de 1.  Cuando la persona comienza, sujeta los aros en la misma tocando su espalda, en ese momento los aros estarían en fase. Tras varias vueltas, en el mismo instante un aro toca el ombligo, sin embargo, el otro aro que gira más rápido está tocando la espalda de la persona, en ese momento los aros no están en fase, están desfasados, hay una diferencia de fase entre ellos. Para ilustrarlo en la siguiente imagen podéis ver muchos aros girando en distintas fases:

Figura 22. Muchos aros girando con diferentes fases unos de otros.

Fenómenos/Propiedades de las ondas

Absorción y Atenuación

Tanto en la absorción como en la atenuación, la amplitud (A) de la onda disminuye, pero por diferentes motivos. Recordemos que la amplitud es la distancia máxima alcanzada por una partícula del medio en cada repetición.

En el caso de la absorción, se produce una disminución de la intensidad y, por lo tanto, de la amplitud de una onda al perder energía mientras se propaga (Giménez Valentín, 2019). Esta perdida se debe a las interacciones con el medio (Giménez Valentín, 2019), como el rozamiento o pérdida en forma de calor. 

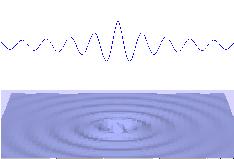Figura 23. atenuación de una onda superficial y representación de la disminución de su amplitud a medida que se propaga.

Si hablamos de atenuación esa disminución en la amplitud se produce al repartirse su energía en frentes cada vez más amplios (Giménez Valentín, 2019). Este fenómeno lo encontraremos en ondas bidimensionales y tridimensionales, como en el ejemplo de la figura 23, porque al propagarse en dos y tres direcciones respectivamente ocupan progresivamente mayor espacio. En una onda unidimensional el espacio ocupado, cuando esta se propaga, no varía.

Para entenderlo un poco mejor tomaremos la metáfora económica que nos presentan en el siguiente video el profesor de la UPV, Marcos Herminio Giménez Valentín, y su amigo "Jota", que es una cabeza. En el ejemplifican primero la absorción y luego la atenuación:

Video 2. Ejemplo de atenuación y absorción de una onda.

Reflexión y Refracción 

Cuando una onda, que se propaga en un medio, llega a otro medio, se produce un cambio de dirección de la onda incidente y por lo general tendremos dos ondas resultantes, una onda que se refleja y otra onda que se refracta (Rubio Michavila, 2019a). La onda que se refleja vuelve al mismo medio y la onda que se refracta se propaga en un medio distinto.

La reflexión consiste en un cambio de dirección, cuando incide una onda en la superficie limítrofe entre dos medios. La onda reflejada se continúa propagando a través del mismo medio por el que a incidido (Rubio Michavila, 2019a). La velocidad (v) de la onda reflejada y la onda incidente es la misma ya que la velocidad (v) depende del medio y al no cambiar de medio esta se mantiene.  

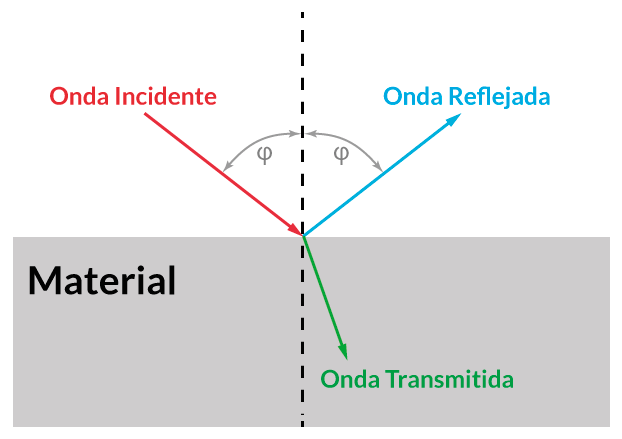Figura 24. Diagrama de la reflexión y refracción de una onda al llegar al límite entre dos medios.

En la imagen superior (figura 24), la onda que pasa al medio gris (verde), y que en el dibujo se denomina "Onda Transmitida", es el resultado de la refracción de la onda incidente (roja). En la refracción se da un cambio de dirección y de medio cuando, una onda incide en la superficie limítrofe entre dos medios. La onda refractada se propagará por el nuevo medio con una velocidad (v) diferente, ya que como habíamos dicho antes, esta depende del medio en que se propaga la onda.

Con esta variación de velocidad (v), el periodo (T) y la frecuencia (f) se conservan sin embargo la longitud de onda (λ) varía, aumentando cuando la velocidad aumente y disminuyendo cuando la velocidad disminuya (Rubio Michavila, 2019b). 

Figura 25. Persona en una fila rebotando entre otras dos. 

Retomemos la metáfora de la fila de niñxs para comprender un poco mejor estos conceptos. El ultimo niño, al que asignamos la posición 5, empuja al que tiene delante: niño número 4. El niño 4 sin poder evitarlo se precipita sobre el 3, que a su vez se precipita sobre el 2 que inevitablemente empuja al 1, que choca contra la puerta. Tras golpearse con la puerta El niño 1 rebota y sin poder evitarlo empuja al niñx 2 que ha su vez empuja al niño tres. Tras golpear la puerta los niños pasan a empujarse en la dirección opuesta a la que lo hacían antes de chocar con la puerta, pero manteniéndose fuera de la clase, esto sería la reflexión del movimiento al llegar a la puerta. Sin embargo, del golpe del niño 1 en la puerta se cae un gorro que está colgado detrás. Parte de la energía con la que el niño 1 ha impactado en la puerta se transmite a esta, la atraviesa y llega al gorro que esta al otro lado. Esto sería el equivalente de la refracción ya que el movimiento ha continuado propagándose por un nuevo medio. 

Difracción

Acabamos de ver qué les pasa a las ondas cuando al propagarse cambian de un medio a otro, y ahora veremos lo que sucede cuando una onda se desvía al atravesar un orificio o encontrar un obstáculo.

El objeto difractante o la rendija, se convierte en una fuente secundaria de la propagación de la onda ("Difracción", 2022). Veremos con más detalle el ejemplo de la rendija, para ello, vamos a recordar que según el principio de Fresnel - Huygens, todo punto de un frente de onda inicial puede considerarse como una fuente de ondas esféricas secundarias.

También, debemos de tener en cuenta que la relación entre la longitud de onda y el tamaño de la rendija van a condicionar la difracción, por eso es necesario que el tamaño de la abertura sea del mismo orden que la longitud de la onda incidente (Rubio Michavila, 2019c). Cuando un frente de ondas llega a una superficie con una rendija del mismo tamaño que su longitud de onda, el punto medio de la rendija se convierte en una fuente puntual de ondas esféricas que se propagan con la misma velocidad, frecuencia y longitud de onda:

Figura 26. Difracción de una onda plana cuando el ancho de la ranura es igual a la longitud de onda.

Si aumentamos el tamaño de la rendija, aparecerán más puntos como fuentes puntuales de ondas esféricas:

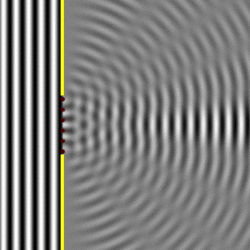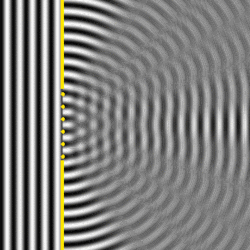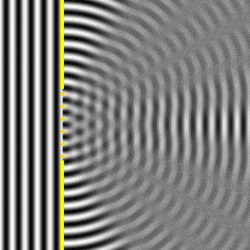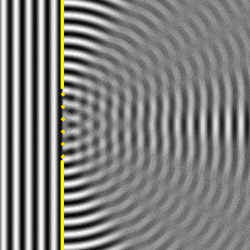Figura 27. Difracción de una onda plana cuando el ancho de la ranura es varias veces la longitud de onda.

Extra: Si el mundo de las ondas os ha apasionado y queréis saber más en el siguiente link podéis encontrar un curso detallado de la UPV sobre oscilaciones y ondas.

Figuras:

Figura 1. Niñx vibrando con un aro. https://giphy.com/gifs/fail-kid-hula-hoop-cIhzInb5BWjXJhREXk 

Figura 2. Representación de dos modos de vibración periódica. https://massbateria.com/modos-de-vibracion-2/

Figura 3. Persona bailando el hula hoop https://giphy.com/gifs/thisgirlcan-hula-hoop-hooping-this-girl-can-JTbqfw3dydAg6d8axU

Figura 4. Amplitud del movimiento del aro en una persona bailando un hula hoop. Imagen editada. https://www.kindpng.com/imgv/ihmTThR_person-using-hula-hoop-hd-png-download/ 

Figura 5. Niñx vibrando. La vibracion no se transmite al aro.  https://giphy.com/gifs/fail-kid-hula-hoop-fSdPI1jp98tlg6xpZS?utm_source=media-link&utm_medium=landing&utm_campaign=Media%20Links&utm_term=https://giphy.com/ 

Figura 6. Fila de personas calends por el empuje de la última. https://giphy.com/gifs/peterbjornandjohn-peter-bjorn-and-john-3o6gE57nEDKeoCxsrK 

Figura 7. Amplitud (A) y periodo (T) en una onda representada en función del tiempo. https://es.wikipedia.org/wiki/Per%C3%ADodo_(f%C3%ADsica)

Figura 8. Representación de una onda periódica (izquierda) y de una onda no periódica (derecha). http://ondassonorasfaviotorrealba.blogspot.com/2015/11/segun-el-medio-en-que-se-propagan.html 

Figura 9. Onda unidimensional. https://intothecontinuum.tumblr.com/post/29160638835/is-it-possible-to-visualize-3-dimensional-standing 

Figura 10. Onda bidimensional. https://intothecontinuum.tumblr.com/post/29165448842/the-end-of-this-post-concludes-with-a 

Figura 11. Onda tridimensional. https://intothecontinuum.tumblr.com/post/29165448842/the-end-of-this-post-concludes-with-a 

Figura 12. Movimiento de una onda longitudinal (arriba) y de una onda transversal (abajo). https://www.physicslens.com/wp-content/uploads/2022/03/longitudinal-transverse-waves.gif 

Figura 13. Partes de una onda. https://www.lifeder.com/onda-transversal/

Figura 14. Representación de una onda en función del espacio (arriba) y una onda en función del tiempo (abajo). https://www.google.com/url?sa=i&url=http%3A%2F%2Fhyperphysics.phy-astr.gsu.edu%2Fhbasees%2FSound%2Fwavplt.html&psig=AOvVaw022BZbBkeoNNzkiuTa9JBV&ust=1665140039984000&source=images&cd=vfe&ved=0CAwQjRxqFwoTCKD91pe4y_oCFQAAAAAdAAAAABAD 

Figura 15. Frente de onda en una onda circular(arriba) y en una onda plana (abajo). https://www.aplustopper.com/what-is-wave/ 

Figura 16. Representación del principio de Fresnel-Huygens en una onda plana (izquierda) y en una onda circular (derecha). https://tfgonline.es/principio-de-huygens/ 

Figura 17. Dos ondas con diferente dirección de desplazamiento. http://ondassonorasfaviotorrealba.blogspot.com/2015/11/segun-el-medio-en-que-se-propagan.html 

Figura 18. Resultado de la superposición de las ondas de la figura 17. http://ondassonorasfaviotorrealba.blogspot.com/2015/11/segun-el-medio-en-que-se-propagan.html 

Figura 19. Representación de la fase de una onda. (Phase=fase, Wave=onda). https://www.nist.gov/image/phasegif 

Figura 20. Representación de la diferencia de fase entre dos ondas con la misma frecuencia. (Phase=fase, Wave=onda). https://www.nist.gov/image/phase-differencegif 

Figura 21. Resultado de la suma de dos ondas sinusoidales de la misma frecuencia, pero diferencia de fase variable. https://mriquestions.com/what-is-phase-encoding.html 

Figura 22. Muchos aros girando con diferentes fases unos de otros. https://giphy.com/gifs/hooping-hula-perth-MwC8t7MaaR7kCr3FaN 

Figura 23. atenuación de una onda superficial y representación de la disminución de su amplitud a medida que se propaga. http://newton.cnice.mec.es/materiales_didacticos/ondas2/ondas-conclusion4.html?3&2  

Figura 24. Diagrama de la reflexión y refracción de una onda al llegar al límite entre dos medios. https://www.prored.es/la-reflexion-en-las-ondas-y-radioenlaces/ 

Figura 25. Persona en una fila rebotando entre otras dos. https://giphy.com/gifs/bully-harold-lloyd-waiting-in-line-26AHRsTEXSMgl3rXi 

Figura 26. Difracción de una onda plana cuando el ancho de la ranura es igual a la longitud de onda. https://es.wikipedia.org/wiki/Principio_de_Fresnel_-_Huygens 

Figura 27. Difracción de una onda plana cuando el ancho de la ranura es varias veces la longitud de onda. https://es.wikipedia.org/wiki/Principio_de_Fresnel_-_Huygens 

Videos: 

Video 1. Superposición de ondas superficiales en el agua. https://www.youtube.com/watch?v=1mPYQ5DVPxQ&t=7s 

Video 2. Ejemplo de atenuación y absorción de una onda. https://www.youtube.com/watch?t=114&v=I4tCNpnR-b4&feature=emb_imp_woyt 

Referencias:

Crowell, B. (2000). Vibrations and waves (Vol. 3). Light and Matter.

Difracción. (2022, abril 23).  En Wikipedia. https://es.wikipedia.org/wiki/Difracci%C3%B3n

French, A. P. (1971). Vibrations and Waves. CRC Press.

Gimenez Valentin, M. H. [Universitat Politècnica de València UPV]. (2019, 30 abril). Atenuación y absorción de una onda | 15/25 | UPV. [Video]. YouTube. https://www.youtube.com/watch?v=I4tCNpnR-b4&t=114s 

Onda. (2021, julio 15). Estefania Coluccio Leskow, En Enciclopedia Concepto. Consultado el 1 octubre 2022 en https://concepto.de/onda-2/ 

Onda. (2022, septiembre 21).  En Wikipedia. https://es.wikipedia.org/wiki/Onda#:~:text=La%20teor%C3%ADa%20de%20ondas%20se,Ostrovsky%20y%20Potapov%2C%201999)

Polyakov, S. (2022, Enero 25). New Telecom Receiver System Checks Reliability of Message Components in Real Time. National Institute of Standards and Technology. https://www.nist.gov/news-events/news/2022/01/new-telecom-receiver-system-checks-reliability-message-components-real-time

Principio de Fresnel - Huygens. (2020, agosto 20) En Wikipedia. https://es.wikipedia.org/wiki/Principio_de_Fresnel_-_Huygens 

Rubio Michavila, C. [Universitat Politècnica de València UPV].  (2019a, 30 abril). Reflexión de las ondas | 18/25 | UPV. [Video]. https://www.youtube.com/watch?v=m32o8WTXy-g&list=PL6kQim6ljTJudzpws0ggAtF0RQsIPwgGr&index=18 

Rubio Michavila, C. [Universitat Politècnica de València UPV].  (2019b, 30 abril b). Refracción de ondas. | 19/25 | UPV. [Video]. https://youtu.be/mXoVi8mv15Y 

Rubio Michavila, C. [Universitat Politècnica de València UPV].  (2019b, 30 abril c). Difracción de ondas. Lección 19 | 20/25 | UPV [Video]. https://youtu.be/vivFGdGVItQ 

Vibración. (2022, septiembre 16). En Wikipedia. https://es.wikipedia.org/wiki/Vibraci%C3%B3n