6.2.6 Ejemplos prácticos en la enseñanza de Matemáticas

Los ejemplos que aquí se van a mencionar se basan en experiencias realmente llevadas al aula. Pero no están reproducidos fielmente, sino que se ha optado por bosquejar las líneas para que se pueden utilizar como ideas de cara a diseñar nuevas actividades.

Simulación

La actividad consiste, básicamente, en responder a cuestiones del tipo:

• ¿Cuánto tengo que esperar a que salga un seis en un dado?
• Si tengo tres tarjetas con las letras A, I y V, y las saco de una bolsa una detrás de otra, ¿cuántas veces tendré que repetir el experimento para que me salga la palabra VIA?
• El problema clásico de los patos y los cazadores (o alguna versión más adecuada para estos tiempos, por ejemplo, con globos y dardos), en el que 10 (o 6 o...) cazadores que nunca fallan, disparan al azar a 10 (o 6 o ...) patos, sin que cada uno sepa a que pato dispara cada uno. Se trata de calcular la media de patos que quedan vivos.
• La variación del anterior: completar la colección.
• Etc.

Además de los conceptos matemáticos que hay debajo, se trata de trabajar la simulación aleatoria como herramienta válida para obtener conclusiones reales. Conviene conectar esta parte con simuladores que ellos pueden utilizar (como los juegos que simulan deportes), con simuladores de vuelo o con simulaciones que puede hacer una empresa para saber si un producto determinado puede funcionar.

Aparte de las simulaciones que se puedan hacer manipulativamente (que nunca está de más), cuando se trata de obtener una gran cantidad de datos conviene acudir a la tecnología. Estas dos páginas <https://echaloasuerte.com/> y <http://sapm.es/petrus/azar/> son solo dos de las muchas que se pueden usar para esta tarea.

Hemos puesto al alumnado en grupos de 4. Como se trata de recopilar muchos datos, es muy importante que cada uno haga su parte de trabajo. Apelamos a su responsabilidad, pues el hecho de que una persona no haga su trabajo repercute negativamente en el colectivo.

Para los cálculos, debemos compartir con toda la clase una hoja de cálculo que previamente hemos preparado, en la que cada uno mete los datos que ha obtenido. La hoja muestra en tiempo real como van variando los resultados a medida que se meten nuevos datos. Se observa la evolución del resultado con los datos individuales, con los del grupo pequeño y con los de la clase. Es sencillo comprobar que haber trabajado todos juntos, haber aportado todos, nos ha permitido obtener un resultado que de otra manera sería o complicado (si lo hacemos de manera teórica) o tedioso (si una sola persona tiene que recopilar todos los datos). También es muy visual cuando un grupo no "cumple"; en un tono distendido, se les hace ver que si nos pagaran por hacer un trabajo de "este estilo" esa falla repercutiría en nuestra remuneración.

Algoritmos históricos

Un aspecto importante a trabajar en nuestro alumnado es que sea consciente de que todos los saberes de nuestra sociedad actual provienen de una serie de conocimientos que se han ido desarrollando desde hace muchos años. Y, lo que es más importante, que lo han hecho interconectándose unos con otros, de tal forma que es complicado entender la evolución de la ciencia sin conocer las condiciones históricas en las que tuvieron lugar cada hito. Cada descubrimiento importante no es un hecho aislado, sino que se produce en un contexto determinado que, en cierta forma, lo provoca o facilita. Huelga decir, que la propia evolución del lenguaje repercute en el lenguaje matemático y viceversa.

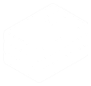
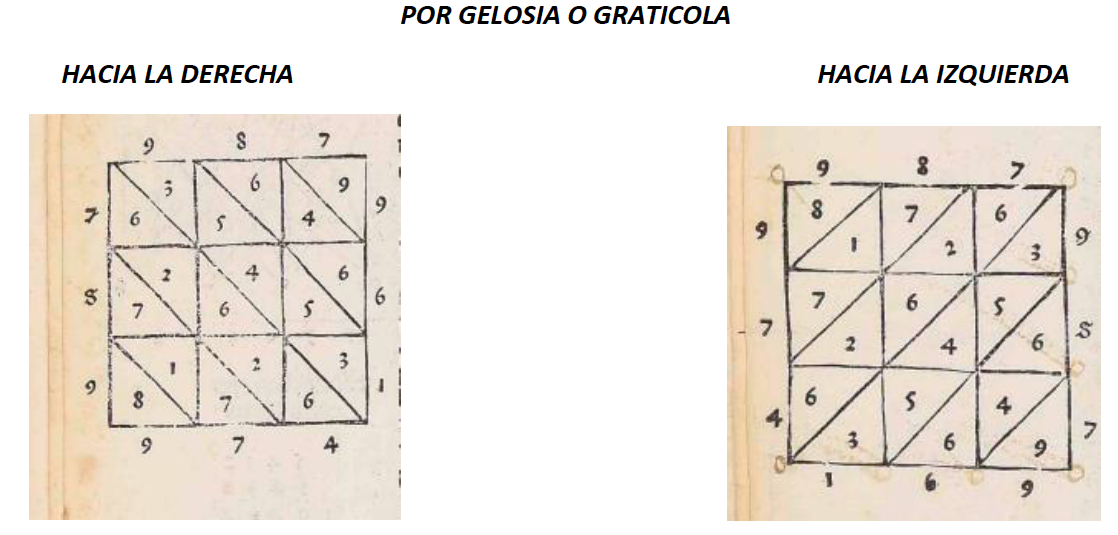
La actividad empieza proporcionando al alumnado una serie de documentos históricos que muestra como se hacían algunas operaciones en alguna etapa concreta de la historia. Por ejemplo.

 

 

 

 

 

 

 

 

 

 

El alumnado, por grupos de 4, debe descubrir, primero, qué operación aritmética se está realizando y, segundo, cómo funciona.