Herramientas para Matemáticas
En el apartado 2.1 se presentaron una serie de enlaces donde buscar recursos digitales ya creados. En muchos de ellos, existen actividades preparadas para retroalimentar las interacciones del alumnado, de tal forma que él mismo pueda "evaluar" en cierta medida su aprendizaje. Aunque, bien es cierto, en muchas ocasiones el recurso se limita a dar la respuesta correcta, lo cual puede no ser útil en el sentido de que el alumno sepa qué es lo que no está entendiendo bien. De todas esas referencias que se dieron, hemos de insistir en que las actividades que se crearon en el marco del proyecto Gauss <http://geogebra.es/gauss/indice.htm> son valiosas también en el sentido tratado en este apartado.
Por otra parte, en el apartado 2.2 se hablaba de varias herramientas para crear generar nuevos contenidos digitales. Lógicamente, el docente puede plantear las actividades que él mismo cree (GeoGebra, Desmos…) de tal forma que que el alumnado pueda autorregular su aprendizaje. Aunque es cierto que esto requiere unos conocimientos técnicos algo superiores, y un tiempo extra de reflexión de cara a plantear la secuencia didáctica.
No obstante, podemos empezar con planteamientos algo menos ambiciosos, pero enriquecedores. El requerimiento que nos hace el nuevo currículo con respecto a hacer patentes las conexiones de los diferentes sentidos matemáticos, nos abre interesantes caminos. Ilustrémoslo con un par de someros ejemplos. Se puede plantear (por ejemplo en 2.º de ESO) la siguiente cuestión:
Aquí podemos empezar con diferentes tanteos, que puede ser con algún material manipulativo o bien algún material digital que equivalga a ese material manipulativo (por ejemplo, existen geoplanos digitales). Se trata de dirigir al alumnado hacia los polígonos regulares, algo relativamente sencillo si lo hacemos con rectángulos. A partir de ahí, pueden calcular a mano áreas del triángulo equilátero, del cuadrado y del hexágono. Les podemos pedir que los dibujen en GeoGebra y que utilicen la herramienta de calcular áreas para comprobar que los cálculos a mano son correctos. Lógicamente, aquí tenemos como objetivo que ellos vayan aprendiendo a utilizar las herramientas informáticas para "monitorizar" su aprendizaje. El resto de polígonos son más complicados; aquí se nos abren varias opciones. Una, sería construirlos con GeoGebra y calcular el área. Otra, es utilizar un libro de espejos para estimar la apotema; la usamos para calcular áreas y lo comprobamos con GeoGebra.
Dando un paso más, ahora contamos con una serie de pares de números (lado, área) y seguimos queriendo saber cuál es la figura geométrica que tiene área máxima con el perímetro dado. Podemos pedirles que representen todos los pares de puntos en GeoGebra (podemos tener un montón de áreas de polígonos, ya que construirlos con GeoGebra es sencillo y rápido); sin ninguna duda "verán" la función y además que se aproxima a un valor, es decir que no crece indefinidamente. Nos está sirviendo la tecnología para aprehender intuitivamente el concepto de asíntota. El profesor debe hacer patente las diferentes conexiones realizadas y las ventajas que supone introducir las herramientas digitales para mejorar cómo y cuánto aprendemos.
En el siguiente ejemplo seremos mucho más breves
Estamos en un curso más avanzado (3º o 4º) y el alumnado ya tiene cierta práctica en el manejo de GeoGebra. La construcción que pide el enunciado no es difícil de hacer. Otro asunto es justificar que en efecto triseca el ángulo recto. Si les pedimos que lo justifiquen (lógicamente sin usar la herramienta de medir ángulos), es posible que se valgan de las mismas herramientas de GeoGebra para intentar razonar la respuesta; es decir, están usando herramientas conocidas para adquirir nuevos conocimientos.
Esto son solo dos ejemplos. Todas las herramientas presentadas en el citado apartado 2.2 permiten actuaciones del mismo estilo, con una intervención activa del profesorado, el alumnado avanza en el proceso del autoaprendizaje. Por mencionar algo más, es de destacar que Threejs (además de trabajar el pensamiento computacional) obliga al alumnado a reflexionar sobre aspectos de geometría del espacio, pues necesita entender bien los conceptos para realizar las construcciones. Y viceversa; la necesidad de plasmar en pantalla lo que quiere construir le va a forzar a profundizar en la parte matemática.
Además de las citadas herramientas, hablaremos ahora de otras tres en las que el alumnado sí que puede trabajar de manera totalmente autónoma, ya que les proporcionan oportunidades para regular tanto el ritmo de aprendizaje como la profunidad
Symbolab
Este programa es similar al más conocido PhotoMath. Es seguro que la mayoría de los alumnos conocen PhotoMath y queramos o no, lo van a usar. Al igual que ocurría con las calculadoras, por mucho que el profesorado las prohiba en algunos cursos, ellos las usan en casa o incluso en el centro, haciendo los deberes durante una guardia. Así que es mejor que seamos nosotros los que les demos las pautas de cómo, cuando y para qué utilizar estas herramientas tecnológicas (calculadora, Symbolab…), para que lo hagan de manera adecuada y les sean útiles para aprender.
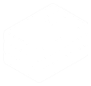
Symbolab es un programa de cálculo, que ofrece soluciones paso por paso. Existe versión para dispositivos móviles, pero para acceder a todas sus funcionalidades es necesario pagar. La alternativa es usar la versión online para ordenadores accediendo a la página web <https://es.symbolab.com/>.
El manejo apenas requiere aprendizaje pues la forma de introducir lo que queremos resolver es, en general, muy natural. ¿En qué puede ayudar este tipo de herramienta para la competencia que estamos trabajando en este área? Ofrece varios aspectos interesantes para que el alumnado pueda trabajar autónomamente, detecte sus errores y aprenda a enmendarlos. Por una parte, muestra la solución paso por paso y, en la mayoría de los casos, de una manera similar a cómo lo haríamos en clase. También se le puede pedir que no podamos ver de golpe todos los pasos sino que aparezcan uno a uno. Al final de la resolución también nos muestra la representación gráfica (desde una ecuación de segundo grado a un límite o una integral definida), lo que ayudará al alumnado a conectar los diferentes sentidos matemáticos. Además, el programa sugiere nuevos "problemas". Por ejemplo, si empiezo a escribir una ecuación de segundo grado que quiero resolver, la herramienta me sugiere varias ecuaciones, lo que hace también al final de la pantalla cuando termina la resolución de la que le he pedido. De esta manera, cualquier persona que quiera practicar más, no necesita que el profesor le siga proporcionando material, pues aquí encontrará enunciados y soluciones.
Tal y como se ha comentado al inicio de este apartado, como siempre el papel del profesorado es crucial. En este caso, para enseñar a que se haga un uso adecuado, que sirva para mejorar el aprendizaje.
Graspable Math
De esta herramienta ya se ha hablado en el apartado 2.2 de este curso. Allí se comentaba que en la página web <https://activities.graspablemath.com/> se puede trabajar con un perfil de profesor o de alumno. Remitimos a los enlaces que en ese punto se referenciaban.
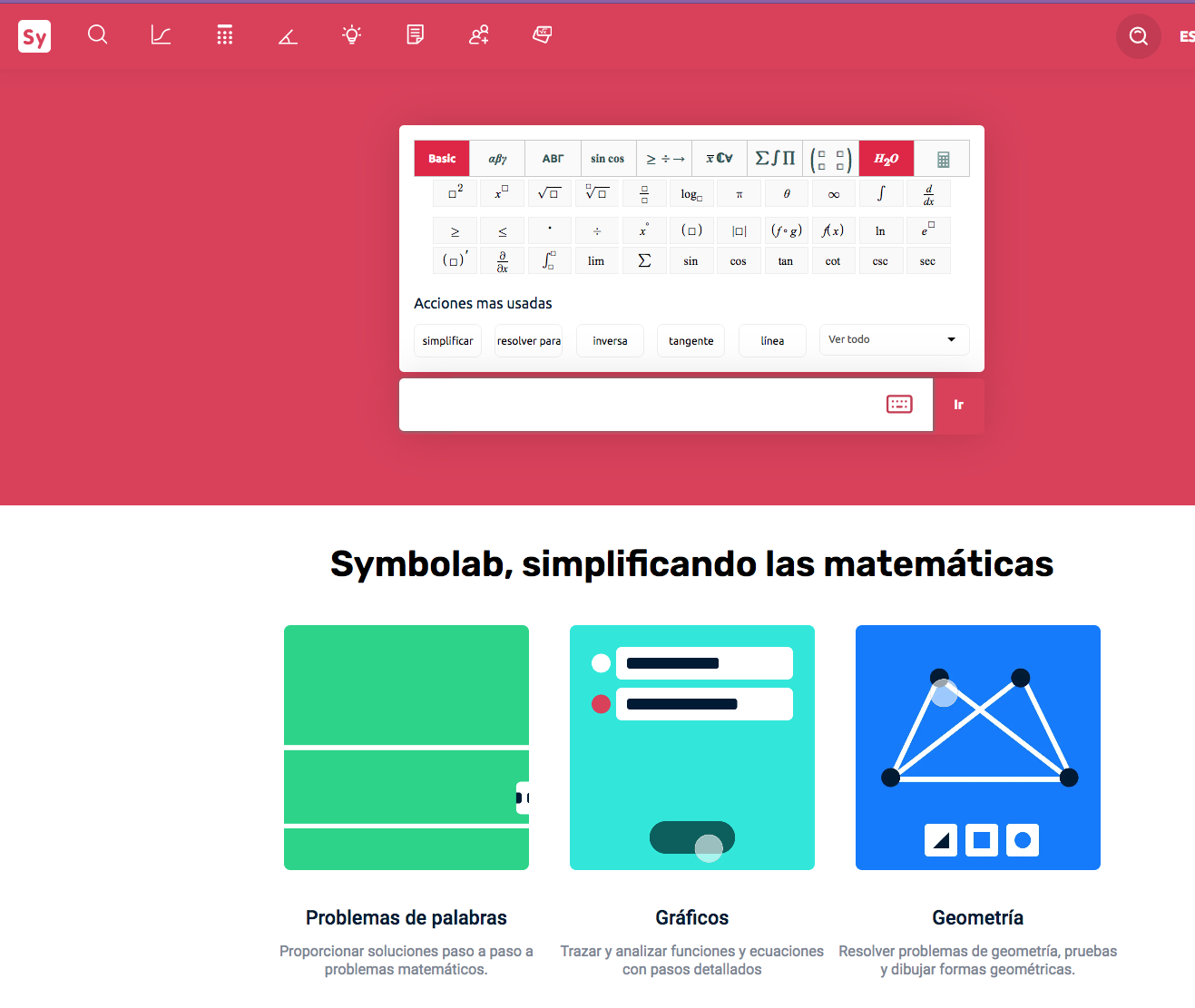
Como se dijo, Graspable está centrado en el aprendizaje de los procedimientos algebraicos en un entorno muy interactivo. Al contrario que Symbolab, el programa no resuelve ecuaciones pero "ayuda" pues no permite acciones prohibidas. También es muy intuitivo a la hora de ingresar las expresiones algebraicas, por lo que su manejo no tiene dificultad. Pongamos un ejemplo sencillos, para intuir las ventajas de la herramienta. Introducimos la siguiente ecuación:
Dando un clic en el signo igual, me aparece un teclado en el que puedo aplicar una operación a ambos lados de la ecuación:
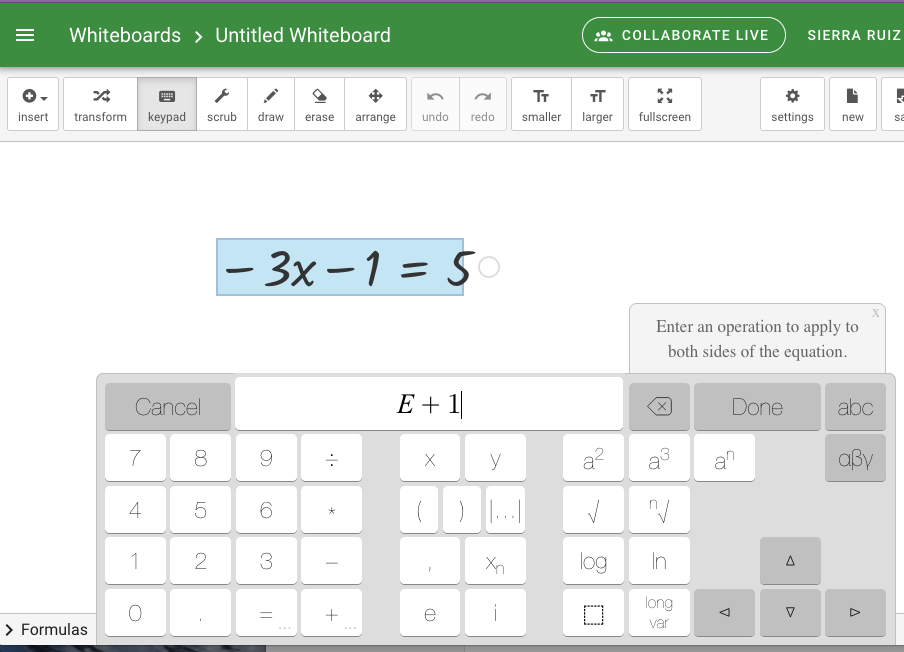
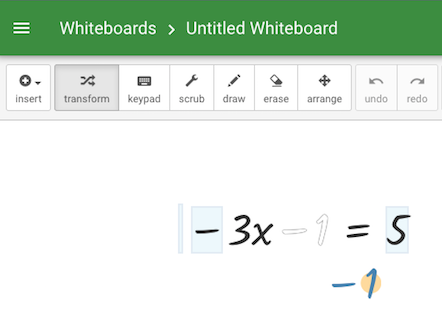
O también puedo pasar (arrastrando con el ratón) el –1 al miembro de la derecha:
Si mi decisión es dividir entre –3: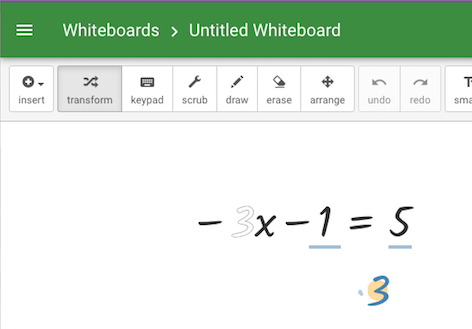
La herramienta lo hace de manera correcta, lo que permite que el alumnado vea como debe hacerlo (y las complicaciones innecesarias que se puede buscar cuando lo haga a mano):
Aquí se pueden repetir los comentarios hechos al respecto del trabajo activo del profesor para que el alumnado use esta herramienta de manera autónoma y pueda autoevaluar su aprendizaje.
Pythagorea
Esta herramienta sirve para trabajar la Geometría de una manera que al alumnado le resulta atractiva. Está diseñada para dispositivos móviles, y al estilo de los juegos, es decir, que para pasar a otra pantalla debes resolver correctamente una previa. No se trata de realizar construcciones geométricas del estilo de los programas de Geometría Dinámica, sino de ir haciendo lo que la app te va pidiendo en cada caso. A continuación se presentan los diferentes apartados con los que cuenta:
Al entrar en uno de ellos, aparece una cuadricula, algunos elementos (puntos, segmentos…) y unas sencillas y breves instrucciones. Por ejemplo, cuadrados, empieza dando cuatro puntos y hay que unirlos (con el dedo) para formar un cuadrado. Progresivamente se va complicando, de tal forma que el alumnado va a tener que ir movilizando sus conocimientos geométricos, necesitará buscar nuevas estrategias y, en algunos casos, realizar algún cálculo.
La app es gratuita y está disponible para Android y para iOS
Podemos sugerírselo al alumnado de manera voluntaria como un divertimento, pero también puede haber una participación más activa del profesorado, preparando una secuencia didáctica. En este último sentido, es interesante visitar el siguiente artículo <https://revistasuma.es/wp-content/uploads/suma/Suma101/S101w_071-078.pdf>.