Curvas cónicas
También disponemos de herramientas para dibujar las cónicas, además de la circunferencia.
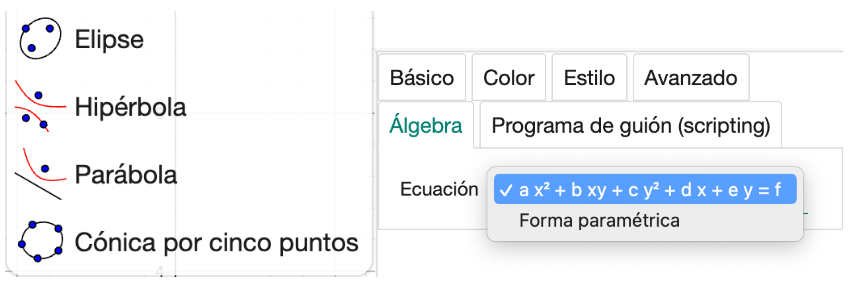
Fig. 2-11 Conjunto de herramientas para dibujar cónicas y tipos de ecuaciones
Con una construcción muy sencilla podemos mostrar las propiedades de las cónicas como lugares geométricos.
- Dibujamos una elipse o una hipérbola, a partir de sus focos y un punto, o una parábola, a partir del foco y su directriz, con la herramienta correspondiente.
- Creamos un punto sobre la curva y, seguidamente, dos segmentos
- que unan este punto con los focos.
- que unan este punto con el foco por un lado y con la intersección de la perpendicular desde el punto a la directriz por otro.
- En la Entrada escribimos
- la suma de los segmentos en el caso de la elipse.
- el valor absoluto de la diferencia de los segmentos en el caso de la hipérbola.
Para la parábola comparamos los dos segmentos con la herramienta “Relación” 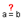 .
.
- Con el botón derecho del ratón clicamos en el punto sobre la curva y, seguidamente, en “Animación”.
- En la Vista Algebraica podemos ver como no se modifican los valores que hemos definido. Una alternativa sería escribir un texto con la propiedad de la curva, pero es un poco más laborioso.
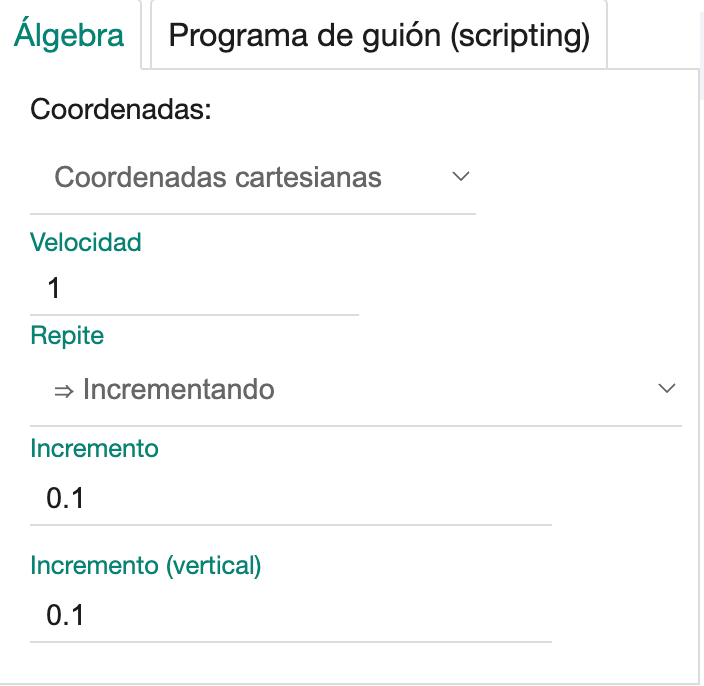
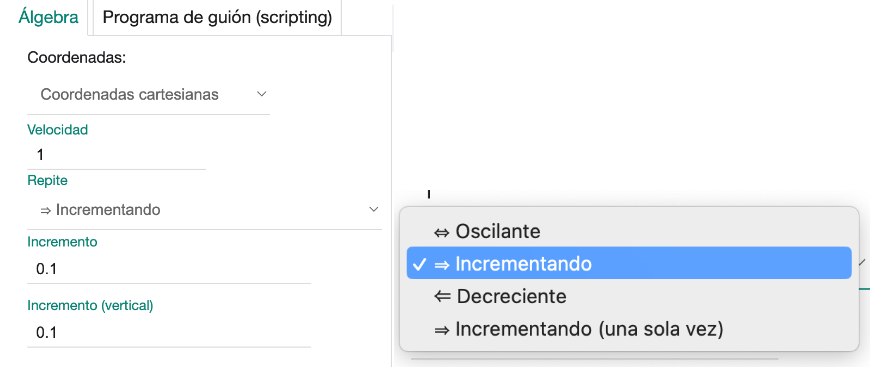
En la configuración del punto que animamos podemos precisar algunos aspectos de la animación en la pestaña “Álgebra”.
Fig. 2-12 Propiedades de la animación de un punto.
La herramienta que crea una cónica por cinco puntos puede ayudar a identificar una curva en determinados problemas o a partir de una imagen. Usando los comandos Foco(Cónica), Ejes(Cónica), EjeMayor(Cónica), EjeMenor(Cónica), LongitudSemiejeMayor(Cónica), LongitudSemiejeMenor(Cónica), Directriz(Parábola) y Tipo(Cónica) en la Entrada con el nombre que ha dado el programa a la cónica tendremos una información completa sobre la curva.