Estudio general de funciones: ceros, máximos, mínimos, puntos de inflexión, concavidad, convexidad, asíntotas...
Puede que tengamos dudas sobre el uso GeoGebra en el aula, pero, en el caso de las funciones, no hay excusa porque es una herramienta que nos facilita enormemente la labor como vamos a ver enseguida.
En primer lugar, escribiremos lo siguiente en la Entrada de la Vista Algebraica:
a x + b (no son necesarios los espacios)
El programa dibuja la función (definiéndola como f(x)) y crea los parámetros a y b como deslizadores (que podemos redefinir en la configuración). Podéis probar esta técnica rápida y sencilla con cualquier función.
El estudio de la función es muy sencillo con GeoGebra.
- Para los ceros de la función tenemos la herramienta “Raíces” . Basta con clicar en la función. También podemos usar la herramienta “Intersección” clicando en el eje X y en la función. Es lo que haremos para los puntos de cortes con el eje Y.
- Para los extremos usaremos la herramienta “Extremos” . Puede no funcionar con determinadas funciones.
- Los intervalos con diferente signo de la función, crecimiento y decrecimiento o concavidad y convexidad se pueden visualizar de la siguiente manera:
- Si(f>0,f)
- Si(f<0,f)
- Si(f’>0,f)
- Si(f’<0,f)
- Si(f’’>0,f)
- Si(f’’<0,f)
- GeoGebra crea cada vez una nueva función. El color lo podemos cambiar en la configuración de la función.
- Para las asíntotas utilizaremos el comando Asíntota(Objeto). Caso de haber más de una asíntota estas aparecerán en una lista entre llaves {}. Para individualizar cada elemento escribiremos (si la lista es l1) l1(1), l1(2) … GeoGebra la interpretará como función.
- Los valores de la función se pueden calcular en la forma habitual: f(valor).
También podemos visualizar el proceso de dibujo de la función creando un punto sobre el eje de abscisas (sea por ejemplo P) y escribiendo (donde inf se interpreta como infinito):
Función(f,-inf,x(P))
Animamos el punto P y vemos como se construye la función. En la Entrada escribimos:
A = (x(P),f(x(P)) que será el punto de la función correspondiente a la abscisa de P.
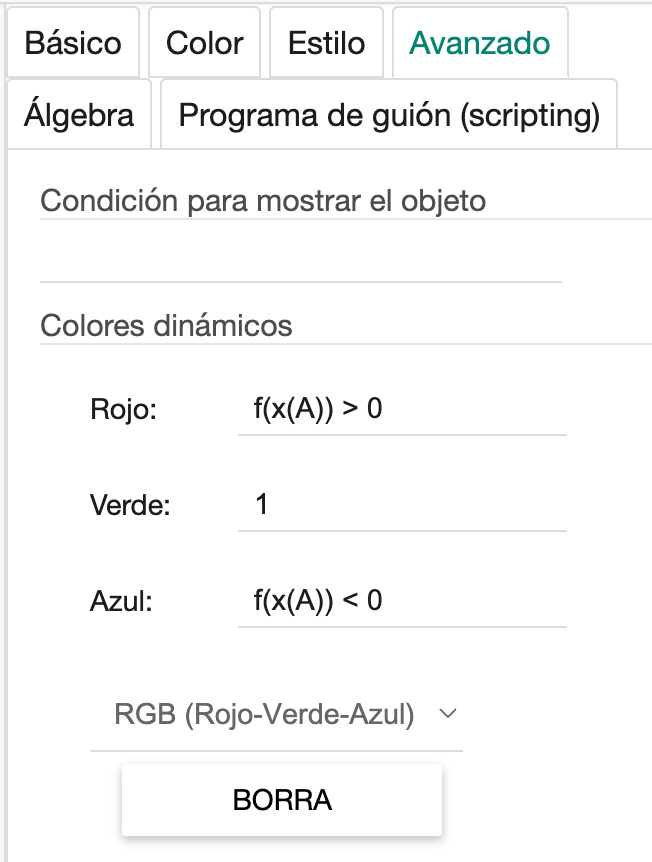
Al punto A le podemos asignar una condición que puede depender del signo de la función, el de la derivada o el de la derivada segunda. Para ello, en la configuración del punto A, en la pestaña Avanzado, en la sección “Color Dinámico” definimos los colores del código RGB como mejor nos convenga. En el ejemplo, si la función en el punto A es positiva, el rojo tendrá el valor 1 y en caso contrario 0. Lo mismo pasará con el color azul cuando la función sea negativa. Las condiciones pueden ser aún más elaboradas mientras tengamos en cuenta la sintaxis de estas (no sirve escribir solo “A”).
Fig. 3-1 Colores dinámicos en la configuración de un punto
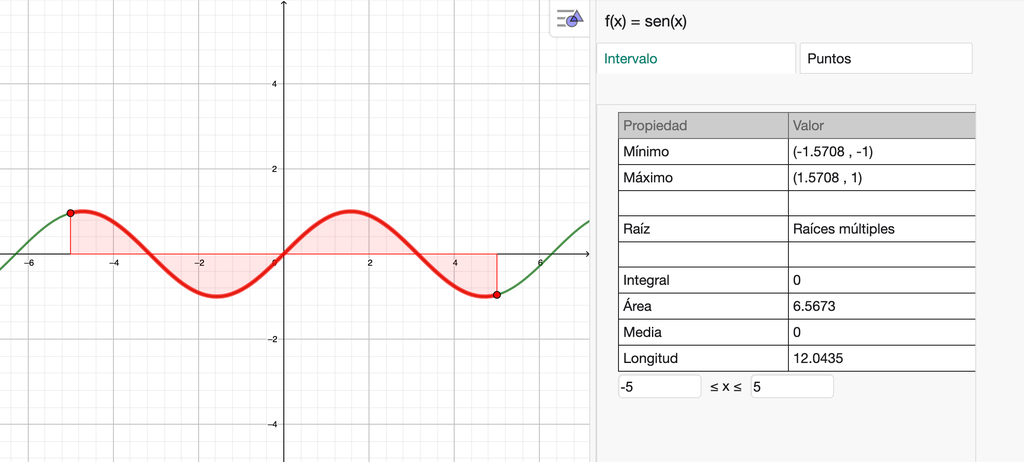
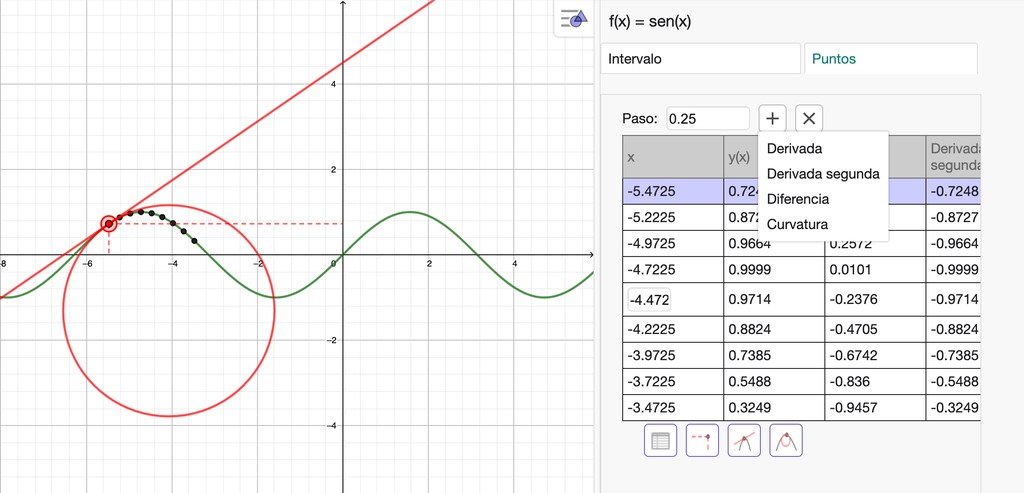
Existe también la posibilidad de usar el “Analizador de funciones”  . Es una herramienta muy completa que incluye una tabla de valores.
. Es una herramienta muy completa que incluye una tabla de valores.
Fig. 3-1a y 1b Analizador de funciones
Basta con clicar en la función una vez seleccionada la herramienta. Su uso es muy sencillo e intuitivo. Podemos modificar el rango de valores moviendo los puntos extremos del intervalo de la función que se destaca en la Vista Gráfica o bien introduciendo los valores en la parte inferior de la ventana del Analizador, en la pestaña “Intervalo”.
En esta lista encontraréis todas las herramientas para las funciones. Y añadimos esta otra (sin actualizar por lo que algunos comandos quizás se hayan modificado o ya no existan) más completa. De hecho, la colección de comandos de GeoGebra es muy completa y se puede hallar aquí. Finalmente, aquí tenéis la lista de operadores y funciones.