Propiedades de los polígonos: cálculo de áreas, estudio de las diagonales...

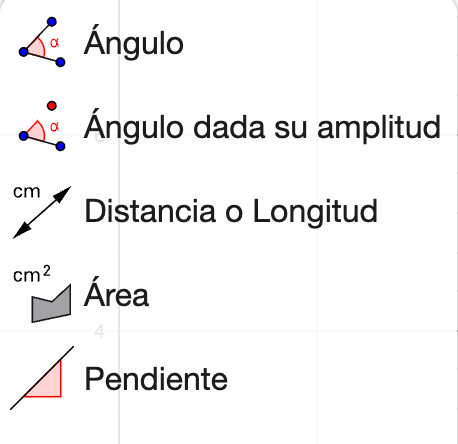
GeoGebra dispone de un conjunto de herramientas de medida que ya hemos utilizado en alguna construcción.

Fig. 2-7 Conjunto de herramientas de medida

Ya tendremos ocasión de hablar de la última de ellas cuando tratemos el tema de las funciones.

En el caso de los polígonos tenemos un amplio abanico de posibilidades para estudiarlos. Veremos un ejemplo muy ilustrativo con polígonos semejantes. Para una construcción más ágil nos adelantaremos al temario y utilizaremos la herramienta “Homotecia”

Dibujamos un polígono con el número de lados que queramos.
Dibujamos un punto en cualquier lugar de la vista gráfica.
Creamos un deslizador con la opción “Número”, Valor mínimo -2, Valor máximo 2 e incremento 0.1.
Con la herramienta “Homotecia”, clicamos en el polígono, luego en el punto que hemos creado y finalmente, en la ventana emergente que nos pide el Factor de escala, introducimos el nombre del deslizador. Nos aparece un nuevo polígono, semejante al anterior. Moved el punto y el deslizador y observad lo que sucede.
Con la herramienta “Punto en objeto” clicamos primero en el interior del polígono inicial y, a continuación, en uno cualquiera de los lados del mismo. Aplicamos la homotecia a los dos puntos con los mismos datos (centro de homotecia y factor de escala) que hemos utilizado para el polígono.
Clicamos con el botón derecho en el punto sobre un lado y activamos la “Animación”. El punto de desplaza por el perímetro del polígono. Con el punto transformado hacemos lo mismo, pero ahora activamos “Mostrar el rastro”.

Para borrar el rastro basta con mover la ruedecita del ratón o bien clicar en la “casita” que retorna la Vista Gráfica a su situación original.

Observad lo que sucede. En la parte inferior izquierda de la Vista Gráfica veréis que aparece un botón de reproducción.
Con el punto en el interior del polígono no podemos activar la animación como es lógico pero sí que podemos ver como se transforma en un punto en el interior del polígono transformado.
Podemos dibujar una diagonal del polígono inicial, poner un punto sobre la misma y ver como de transforma en un punto de una diagonal del polígono transformado.
Ahora ya podemos utilizar las herramientas de medida y comparar las longitudes de los lados, las áreas, las diagonales y los ángulos de ambos polígonos. Moviendo el deslizador se puede ver cómo, aunque cambian los valores, las proporciones siempre son las mismas. Para mostrar esta característica de las figuras semejantes podemos usar un truco de GeoGebra que nos ahorra escribir texto. Nos obliga a tener abierta dicha Vista, pero nos ahorra tiempo. Mejor tener ordenados los objetos por orden de construcción para usar este truco.
- En la Entrada de la Vista algebraica escribimos a’/a (por ejemplo) y saldrá la proporción entre los dos lados de los polígonos.
- A continuación, escribimos polígono1’/polígono1 (o como GeoGebra haya nombrado a los polígonos) y comparamos el resultado con el obtenido para los lados. Para ello utilizaremos los nombres que el programa habrá dado a los cocientes.