Pilares del pensamiento computacional: Reconocimiento de patrones
Descomposición: Divide y vencerás
¿Qué es la descomposición?
Antes de que se pueda resolver un problema, se debe comprender el problema y las formas en que se puede resolver. La descomposición implica dividir un problema o sistema complejo en partes más pequeñas que son más manejables y fáciles de entender. Luego, las partes más pequeñas se pueden examinar y resolver, o diseñar individualmente, ya que es más fácil trabajar con ellas.
¿Por qué es importante la descomposición?
Si un problema no se descompone:
Es mucho más difícil de resolver.Tratar con muchas variables diferentes a la vez es mucho más difícil que dividir un problema en varios problemas más pequeños y resolver cada uno, de uno en uno.Dividir el problema en partes más pequeñas significa que cada problema más pequeño se puede examinar con más detalle.Es mucho más difícil de entender.Tratar de entender cómo funciona un sistema complejo es más fácil fijándose en cada uno de los sub-sistemas.Por ejemplo, entender cómo funciona una bicicleta es más sencillo si toda la bicicleta se separa en partes más pequeñas y se examina cada parte para ver cómo funciona con más detalle.
La descomposición en la práctica
Hacemos muchas tareas a diario sin siquiera pensar en ellas, o descomponerlas, como lavarnos los dientes.
Ejemplo 1: Lavarnos los dientes
Para descomponer el problema de cómo lavarnos los dientes, necesitaríamos considerar:
¿Qué cepillo usar?¿Cuánto tiempo estar cepillándome los dientes?¿Cuánta presión debo hacer con el cepillo?¿Qué pasta usar?
Ejemplo 2: Resolver un crimen
Normalmente, solo cuando se nos pide que hagamos una tarea nueva o más compleja, comenzamos a pensar en ella en detalle, a descomponer la tarea.
Imagina que se ha cometido un crimen. Resolver un crimen puede ser un problema muy complejo ya que hay muchas cosas a considerar.
Por ejemplo, la policía deberá averiguar la respuesta a una serie de problemas menores:
¿Qué crimen ha sido cometido?¿Cuándo fue cometido el crimen?¿Dónde fue cometido el crimen?¿Qué evidencia hay?¿Hay algún testigo?¿Han ocurrido crímenes similares?
El problema complejo de resolver el delito cometido ahora se ha descompuesto en problemas más simples que pueden ser examinados individualmente, en detalle.
Ejemplo 3: Crear una aplicación
Imagínate que vas a crear tu primera aplicación. Este es un problema complejo en el que hay un montón de cosas a considerar.
¿Cómo descompondrías la tarea de crear una app?
Para descomponer esta tarea, necesitarás encontrar la respuesta a una serie de problemas menores:
¿Qué necesita para cubrir tu aplicación?¿Qué aspecto tendrá tu app?¿Quién es el objetivo público de tu app?¿Qué tipo de gráficos usarás?¿Qué tipo de audio usarás?¿Qué tipo de software usarás para crear la app?¿Cómo navegará el usuario por la aplicación?¿Cómo probarás la aplicación?¿Dónde se venderá la aplicación?
Esta lista ha desglosado el problema complejo de crear una aplicación en problemas mucho más simples, que ahora se pueden resolver. También puedes hacer que otras personas te ayuden con diferentes partes individuales de la aplicación. Por ejemplo, puedes conocer a alguien que pueda crear los gráficos…
IDEA Descomponer tareas cotidianas: prepara un bocadillo, prepara una excursión… (cuanto más cercana sea la tarea a la experiencia del alumnado mejor).
IDEA Descomponer una figura geométrica en figuras sencillas ya conocidas.
IDEA Jugar al tangram
IDEA hacer mapas mentales
Reconocimiento de patrones: Esto lo he visto antes…
¿Qué es reconocimiento de patrones?
El reconocimiento de patrones es uno de los cuatro pilares del pensamiento computacional. Implica encontrar patrones entre problemas pequeños y descompuestos. A menudo, cuando descomponemos un problema complejo encontramos patrones entre los problemas más pequeños que creamos. Identificar estas similitudes nos ayuda a resolver problemas más complejos de manera más eficiente. Los patrones son pues, similitudes, estructuras repetitivas, características comunes…
¿Qué son patrones?
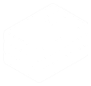
Imagina que queremos dibujar una serie de gatos.
Todos los gatos comparten características comunes. Entre otras cosas, todos tienen ojos, cola y pelaje. También les gusta comer pescado y maullar.
Como sabemos que todos los gatos tienen ojos, cola y pelaje, podemos hacer un buen intento de dibujar un gato simplemente incluyendo estas características comunes.
En el pensamiento computacional, estas características se conocen como patrones. Una vez que sabemos cómo describir un gato, podemos describir otros, simplemente siguiendo este patrón. Lo único que es diferente son los detalles:
- Un gato puede tener ojos verdes, cola larga y pelaje negro.
- Otro gato puede tener ojos amarillos, cola corta y pelaje rayado.
¿Porqué necesitamos buscar patrones?
Encontrar patrones es extremadamente importante. Los patrones simplifican nuestra tarea. Los problemas son más fáciles de resolver cuando comparten patrones, porque podemos usar una misma resolución donde exista un determinado patrón.
Cuantos más patrones podamos encontrar, más fácil y rápida será nuestra tarea general de resolución de problemas.
Si queremos dibujar varios gatos, encontrar un patrón para describir a los gatos en general, como por ejemplo que todos tienen ojos, cola y pelaje, hace que esta tarea sea más rápida y sencilla.
Sabemos que todos los gatos siguen este patrón, así que no tenemos que detenernos cada vez que empezamos a dibujar un nuevo gato para resolver esto. A partir de los patrones que sabemos que siguen los gatos, podemos dibujar rápidamente varios gatos.
¿Qué ocurre cuando no buscamos un patrón?
Supongamos que no hubiéramos buscado patrones en los gatos. Cada vez que quisiéramos dibujar un gato, tendríamos que detenernos y averiguar cómo era un gato. Esto nos retrasaría.
Aún así, podríamos dibujar a nuestros gatos, y se reconocerían como gatos, pero tardaríamos más en dibujar cada gato. Esto sería muy ineficiente y una mala manera de resolver la tarea de dibujar gatos.
Además, si no buscamos patrones, es posible que no nos demos cuenta de que todos los gatos tienen ojos, cola y pelaje. Cuando están dibujados, es posible que nuestros gatos ni siquiera parezcan gatos. En este caso, al no reconocer el patrón, estaríamos resolviendo el problema incorrectamente.
Reconocimiento de patrones dentro del mismo problema o entre problemas diferentes
Para encontrar patrones en problemas buscamos elementos que son iguales (o muy similares) en cada problema. Puede resultar que no existan características comunes entre los problemas, pero aun así deberíamos buscar.
Existen patrones entre diferentes problemas y dentro de problemas individuales. Tenemos que buscar los dos.
Patrones entre diferentes problemas
Para encontrar patrones entre problemas, buscamos cosas que sean iguales (o muy similares) para cada problema.
Por ejemplo, descomponer la tarea de hornear un pastel supone que conozcamos las soluciones a una serie de problemas más pequeños:
- Qué tipo de pastel queremos hornear
- Qué ingredientes necesitamos y cuánto de cada uno
- Para cuántas personas queremos hacer el pastel
- Cuánto tiempo tenemos que hornear el pastel
- Cuándo necesitamos agregar cada ingrediente
- Qué equipo necesitamos
Una vez que sabemos cómo hornear un tipo particular de pastel, podemos ver que hornear otro tipo de pastel no es tan diferente, porque existen patrones.
Por ejemplo:
- Cada pastel necesitará una cantidad precisa de ingredientes específicos.
- Los ingredientes se agregarán en un momento concreto.
- Cada pastel se horneará durante un período de tiempo concreto.
Tenemos los patrones identificados, podemos trabajar en soluciones comunes entre los problemas.
Patrones dentro de los problemas
Los patrones también pueden existir dentro de los problemas más pequeños, en los que hemos descompuesto el problema.
Si nos fijamos en hornear un pastel, por ejemplo, para cada pastel se necesitará una cantidad precisa de ingredientes específicos, cada ingrediente necesita:
- Identificar el ingredientes (nombrarlo)
- Una medida específica
Una vez que sabemos cómo identificar cada ingrediente y su cantidad, podemos aplicar ese patrón a todos los ingredientes. Una vez más, todo lo que cambia son los detalles.
El reconocimiento de patrones dentro de un problema es sencillo de ver si nos imaginamos que estamos haciendo un pastel con una niña o niño. Si por ejemplo hacemos un bizcocho cuyos ingredientes son: harina, azúcar, cacao en polvo, levadura, yogurt y huevos. Podemos hacer juntas la tarea de agregar la harina. Miramos la cantidad requerida, la pesamos y la apartamos en un bol. Una vez hecho, puedo pedir a mi compi que haga sola o solo el paso correspondiente al azúcar. Para ello empleará el mismo procedimiento que hemos empleando para la harina, es decir, usará un patrón. Este mismo puede repetirse para otros ingredientes como el cacao o la levadura. Son patrones dentro del mismo problema.
IDEAS. Además de usar soportes tipo ficha como los que usaremos en el módulo 2, puedes utilizar otros soportes y realizar estas actividades de manera transversal en varias asignaturas y eventos escolares. Bloques de construcción: Usando color, forma o ambos elementos. Hacer collares, pulseras, guirnaldas para navidad o la fiesta de fin de curso, elementos para decorar el aula. Patrones musicales y rítmicos: En esta actividad puedes implica todo el cuerpo. Secuencias con plastilina.
Los edificios escolares a menudo siguen patrones, por ejemplo en las baldosa, en cada cuanto hay una ventana, donde están los baños, tal vez los ciclos estén identificados por colores…. podéis jugar a encontrar los de vuestra escuela.
Juegos de mesa tipo el SET. Recomendado para mayores de 6 años y con partidas de entre 10 y 20 min de duración. En él usamos unas cartas con diferentes atributos de color, cantidad, forma y tipo de relleno para crear los patrones y hacer tríos de cartas según los que definamos. Es un juego complejo ya que incluye patrones de diferencia, es decir, yo puedo asociar cartas porque tienen todas el mismo color o porque ningún color esta repetido. A su vez, puedo combinar patrones de igualdad y de diferencia. Puedo hacer un trio donde: todas las cartas tengan el mismo color, no se repita ninguna forma , no se repita ningún fondo y haya la misma cantidad de elementos. Las combinaciones son múltiples. Si no te ha quedado claro, lo mejor es que mires el siguiente video:
Este es un juego competitivo. Esto puede suponer un problema a la hora de llevarlo al aula dependiendo del grupo que tengas y los recursos de los que dispongas. Una variante del juego puede ser que en vez de jugar a ver quién hace más sets sea a ver cuántos sets pueden hacer entre todas las personas que están jugando en un tiempo limitado.
Abstracción. Me sirve, no me sirve
¿Qué es la abstracción?
Una vez que hemos reconocido patrones en nuestros problemas, usamos la abstracción para reunir las características generales y filtrar los detalles que no necesitamos para resolver nuestro problema para así concentrarnos en las que sí necesitamos.
En el pensamiento computacional, cuando descomponemos un problema, buscamos patrones con problemas similares o dentro del mismo problema que simplifiquen el problema complejo. Cuando abstraemos, filtramos, nos quedamos sólo con la información relevante. A partir de esto creamos una representación (idea) de lo que estamos tratando de resolver.
¿Cuáles son los detalles o características específicas?
En el reconocimiento de patrones, analizamos el problema de tener que dibujar una serie de gatos.
Notamos que todos los gatos tienen características generales, que son comunes a todos los gatos, por ejemplo, ojos, cola, pelaje, gusto por los peces y la capacidad de hacer maullidos. Además, cada gato tiene características específicas, como pelaje negro, cola larga, ojos verdes, amor por el salmón y un fuerte maullido. Estos detalles se conocen como específicos.
Para dibujar un gato básico, necesitamos saber que tiene cola, pelaje y ojos. Estas características son relevantes. No necesitamos saber qué sonido hace un gato o que le gusta el pescado. Estas características son irrelevantes y se pueden filtrar.
A partir de las características generales que tenemos (cola, pelaje, ojos) podemos construir una idea básica de un gato, es decir, cómo es básicamente un gato. Es entonces cuando podemos describir cómo dibujar un gato básico.
¿Por qué la abstracción es importante?
La abstracción nos permite crear una idea general de cuál es el problema y cómo resolverlo. El proceso nos indica que eliminemos todos los detalles específicos y cualquier patrón que no nos ayude a resolver nuestro problema. Esto nos ayuda a formar nuestra idea del problema. Esta idea se conoce como un "modelo".
Si no abstraemos, podemos terminar con una solución incorrecta al problema que estamos tratando de resolver. Con nuestro ejemplo del gato, si no hiciéramos abstracción, podríamos pensar que todos los gatos tienen colas largas y pelaje corto. Habiéndonos abstraído, sabemos que aunque los gatos tienen cola y pelaje, no todas las colas son largas y no todo el pelaje es corto. En este caso, la abstracción nos ha ayudado a formar un modelo más claro de un gato.
Cómo abstraer
La abstracción es la recopilación de las características generales que necesitamos y la filtración de los detalles y características que no necesitamos.
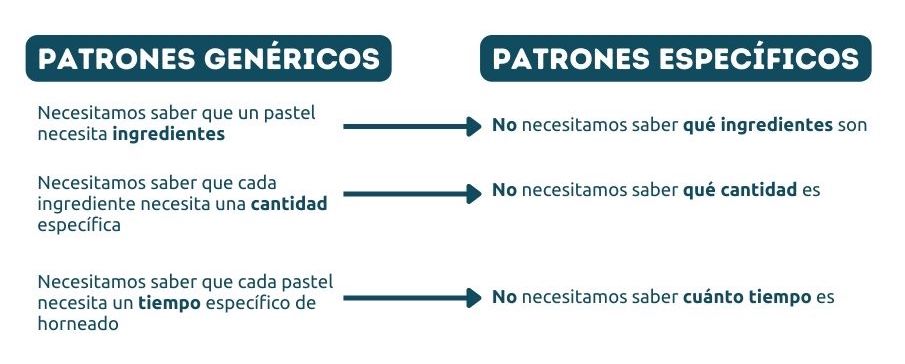
Al hornear un pastel, hay algunas características generales entre los pasteles. Por ejemplo:
- Un pastel necesita ingredientes
- Cada ingrediente necesita una cantidad específica
- Un pastel necesita un tiempo de horneado
Al abstraer, eliminamos detalles específicos y mantenemos los patrones generales relevantes.
 Creando un modelo
Creando un modelo
Un modelo es una idea general del problema que estamos tratando de resolver
Por ejemplo, un gato modelo sería cualquier gato. No es un gato específico con cola larga y pelaje corto: el modelo representa a todos los gatos. A partir de nuestro modelo de gatos, podemos aprender cómo es cualquier gato, usando los patrones que comparten todos los gatos.
Del mismo modo, al hornear un pastel, un pastel modelo no sería un pastel específico, como un bizcocho o un pastel de frutas. En cambio, el modelo representaría todos los pasteles. A partir de este modelo podemos aprender a hornear cualquier pastel, utilizando los patrones que se aplican a todos los pasteles.
Una vez que tenemos un modelo de nuestro problema, podemos diseñar un algoritmo para resolverlo.
Algoritmos. Vamos paso a paso
Un algoritmo es un plan, un conjunto de instrucciones paso a paso para resolver un problema. En un algoritmo se identifica cada instrucción y se planifica el orden en que se deben ejecutar.
¿Qué es un algoritmo?
Los algoritmos son uno de los cuatro pilares del pensamiento computacional. Un algoritmo es un plan, un conjunto de instrucciones paso a paso para resolver un problema. Si puedes atarte los cordones de los zapatos, preparar una taza de té, vestirte o preparar una comida, entonces ya sabes cómo seguir un algoritmo.
En un algoritmo se identifica cada instrucción y se planifica el orden en el que se deben llevar a cabo. Los algoritmos a menudo se usan como punto de partida para crear un programa de ordenador y, a veces, se escriben como un diagrama de flujo o en pseudo-código.
Si queremos decirle a un ordenador que haga algo, tenemos que escribir un programa informático que le diga al ordenador, paso a paso, exactamente qué queremos que haga y cómo queremos que lo haga. Este programa paso a paso necesitará planificación, y para hacerlo usamos un algoritmo.
Las ordenadores son tan buenos como los algoritmos que se les da. Si introduces en el ordenador un algoritmo deficiente, obtendrás un resultado deficiente.
Los algoritmos se utilizan para muchas cosas diferentes, incluidos los cálculos, el procesamiento de datos y la automatización.
Haciendo un plan
Es importante planificar la solución a un problema para asegurarse de que será correcta. Usando el pensamiento computacional y la descomposición, podemos dividir el problema en partes más pequeñas y luego podemos planificar cómo volver a encajarlo en un orden adecuado para resolver el problema.
Este orden se puede representar como un algoritmo. Un algoritmo debe ser claro.
Debe tener:
- un punto de partida
- un punto de llegada
- un conjunto de instrucciones claras entre ambos.
Representación de un algoritmo: Pseudo-código
Hay dos formas principales en que se pueden representar los algoritmos: pseudo-código y diagramas de flujo.
La mayoría de los programas se desarrollan utilizando lenguajes de programación. Estos lenguajes tienen una sintaxis específica que debe usarse para que el programa funcione correctamente. El pseudo-código no es un lenguaje de programación, es una forma simple de describir un conjunto de instrucciones que no tiene que usar una sintaxis específica.
Escribir en pseudo-código es similar a escribir en un lenguaje de programación. Cada paso del algoritmo está escrito en una línea propia en secuencia. Por lo general, las instrucciones se escriben en mayúsculas, las variables en minúsculas y los mensajes en forma de oración.
En pseudo-código, ENTRADA hace una pregunta. SALIDA imprime un mensaje en pantalla.
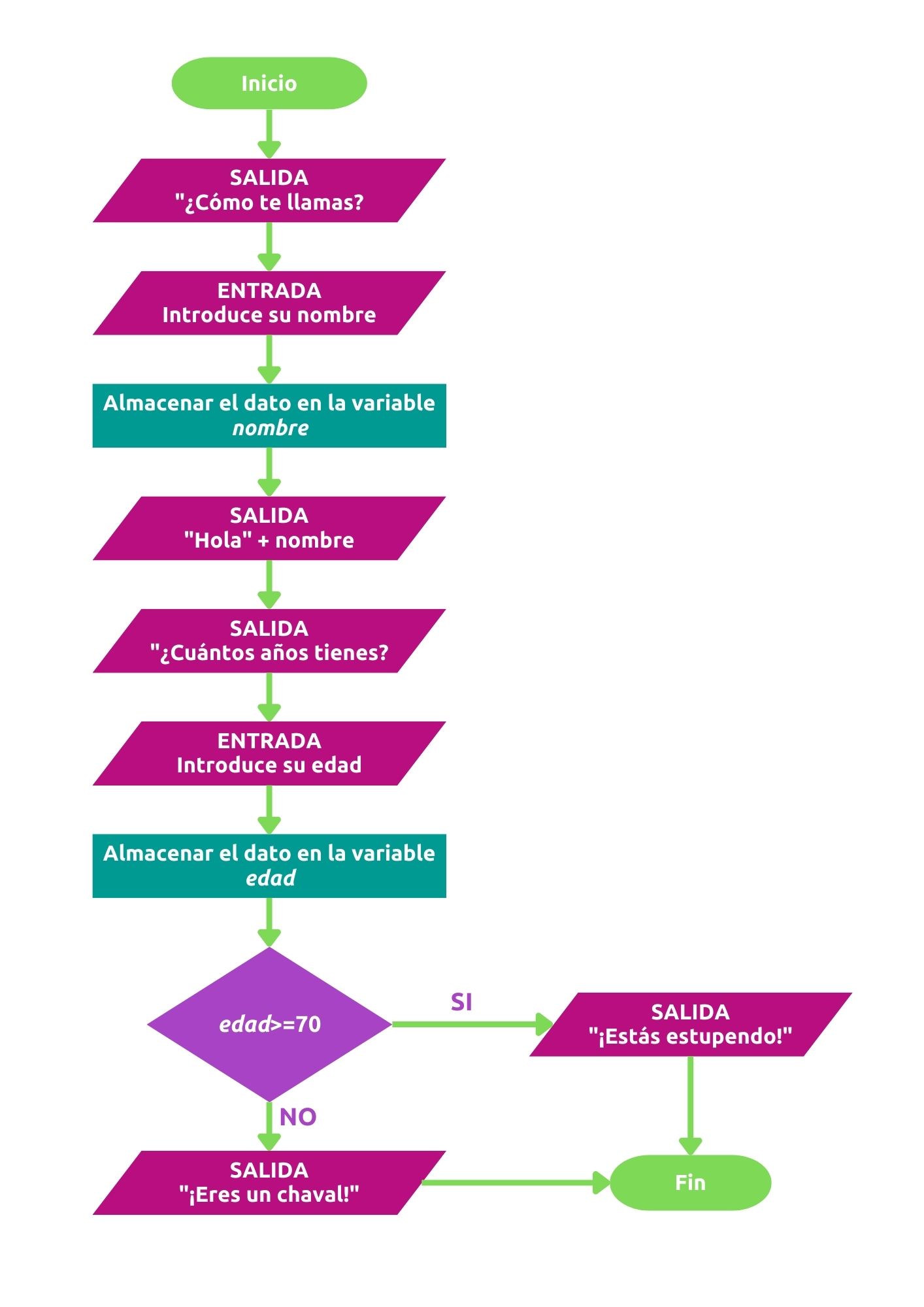
Se podría crear un programa simple para preguntarle a alguien su nombre y edad, y hacer un comentario basado en esto. Este programa representado en pseudo-código tendría este aspecto:
SALIDA “Cómo te llamas?”
ENTRADA el usuario introduce, teclea, su nombre
ALMACENAR la entrada del usuario en la variable nombre
SALIDA “Hola” + nombre
SALIDA “¿Qué edad tienes?”
ENTRADA el usuario introduce su edad
ALMACENAR la entrada del usuario en la variable edad
SI edad >= 70 ENTONCES
SALIDA “¡Estás estupendo!”
SI NO
SALIDA “¡Eres un chaval!”
IDEA. Pueden jugar a guiar el dibujo de otra persona. Una persona da las instrucciones, por ejemplo: dibuja un círculo, haz unos triángulos saliendo del círculo, dibuja una casa debajo del círculo…. Puede haber varias personas dibujando lo que una persona indica. Las diferencias entre los dibujos en parte se deberán a la que las instrucciones no han sido lo suficientemente concretas. A medida que jueguen irán afinando las instrucciones, por ejemplo: dibuja un círculo de 3 cm de diámetro en el centro del la hoja, haz 5 triángulos iguales saliendo del círculo. Los triángulos tienen dos lados iguales, la base es el trazado del círculo y no es igual a los lados, dibuja una casa debajo del círculo, compuesta por un tejado triangular igual a los que has dibujado para hacer el sol…. Para facilitar el trabajo puedes ofrecerles papel cuadriculado para hacer esta actividad y entregarles fichas a los que deben describir para que las otras personas dibujen o que lo hagan de manera libre.
IDEA. Hacer un pseudo-código para hacer tareas sencillas, como ir al baño, sacar punta a un lápiz, levantar una silla….. Cada equipo escribe las instrucciones y se las pasa a otro equipo. El otro equipo las tiene que seguir al pie de la letra y hacer solo lo que pone en las instrucciones.
IDEA. Tal vez conozcas el texto de Julio Cortazar “Instrucciones para subir una escalera”. Puede ser divertido escoger textos de instrucciones y usarlos de base para hacer un pseudo-código. O coger un pseudo-código sencillo y convertirlo en un texto difícil de entender cómo es el caso de este cuento. También puedes adaptar el cuento para que no se sepa de qué se habla y jugar a adivinar. A partir de aquí puedes animarles ha hacer su propio cuento , en el que describan una actividad que las demás deban adivinar. Una posibilidad de adaptación podrías ser: “Instrucciones para realizar una tarea misteriosa”: "Nadie habrá dejado de observar que con frecuencia el suelo se pliega de manera tal que una parte sube en ángulo recto con el plano del suelo, y luego la parte siguiente se coloca paralela a este plano, para dar paso a una nueva perpendicular, conducta que se repite en espiral o en línea quebrada hasta alturas sumamente variables. Agachándose y poniendo la mano izquierda en una de las partes verticales, y la derecha en la horizontal correspondiente, se está en posesión momentánea de un segmento. Cada uno de estos segmentos, formados como se ve por dos elementos, se sitúa un tanto más arriba y adelante que el anterior, principio que da sentido a la estructura, ya que cualquiera otra combinación producirá formas quizá más bellas o pintorescas, pero incapaces de cumplir su función. Estas estructuras se encaran de frente, pues hacia atrás o de costado resultan particularmente incómodas. La actitud natural consiste en mantenerse de pie, los brazos colgando sin esfuerzo, la cabeza erguida aunque no tanto que los ojos dejen de ver los peldaños inmediatamente superiores al que se pisa, y respirando lenta y regularmente. Para realizar nuestra tarea misteriosa se comienza por levantar esa parte del cuerpo situada a la derecha abajo, envuelta casi siempre en cuero o gamuza, y que salvo excepciones cabe exactamente en el segmento. Puesta en el primer segmento dicha parte, que para abreviar llamaremos pie, se recoge la parte equivalente de la izquierda (también llamada pie, pero que no ha de confundirse con el pie antes citado), y llevándola a la altura del pie, se le hace seguir hasta colocarla en el segundo segmento, con lo cual en éste descansará el pie, y en el primero descansará el pie. (Los primeros segmentos son siempre los más difíciles, hasta adquirir la coordinación necesaria. La coincidencia de nombre entre el pie y el pie hace difícil la explicación. Cuídese especialmente de no levantar al mismo tiempo el pie y el pie). Llegado en esta forma al segundo segmento, basta repetir alternadamente los movimientos hasta encontrarse con el final de la estructura. Se sale de ella fácilmente, con un ligero golpe de talón que la fija en su sitio, del que no se moverá hasta el momento del descenso"
IDEA. Jugar a ser robots: Se puede jugar por tríos: una persona es un robot tipo BeeBot, otra quien programa y la tercera al ver el código escrito tiene que adivinar a dónde llegará el “robot”. Quien programa escribe la secuencia usando flechas, se lo muestra a quien adivina y este hace una predicción. Luego se “programa” a quien hace de robot haciendo como que tiene una botonera en la espalda ( adelante, atrás, izquierda, derecha). El juego aumenta la dificultad si quien hace de robot tiene los ojos vendados o si pones obstáculos. Facilita el juego hacerlo en un lugar donde haya baldosas o similares que delimiten cuál es la unidad de desplazamiento.
Si no conoces como funciona la Beebot te dejamos un video, podrás ver cómo funciona a partir de el minuto 1: 47
Representación un algoritmo: diagramas de flujo
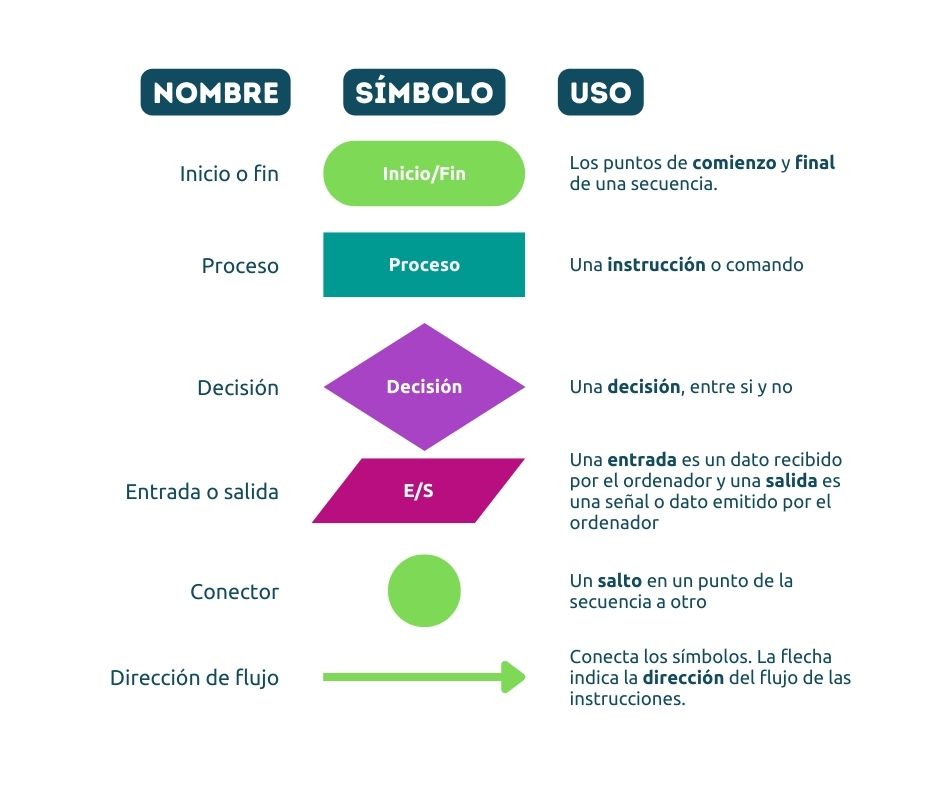
Un diagrama de flujo es una representación de un conjunto de instrucciones. Los diagramas de flujo normalmente usan símbolos estándar para representar las diferentes instrucciones. Hay pocas reglas reales sobre el nivel de detalle necesario en un diagrama de flujo. A veces, los diagramas de flujo se dividen en muchos pasos para brindar muchos detalles sobre lo que está sucediendo exactamente. A veces se simplifican para que una serie de pasos ocurran en un solo paso.
Símbolos del diagrama de flujo
Se podría crear un programa simple para preguntarle a alguien su nombre y edad, y hacer un comentario basado en esto. Este programa representado como un diagrama de flujo se vería así:
 Los diagramas de flujo pueden emplearse para resolver problemas de cualquier naturaleza, sin importa el tema ni la dificultad (de hecho, cuanto más complejo es el problema más útil) Veamos un ejemplo:
Los diagramas de flujo pueden emplearse para resolver problemas de cualquier naturaleza, sin importa el tema ni la dificultad (de hecho, cuanto más complejo es el problema más útil) Veamos un ejemplo:
IDEA. Se pueden crear diagramas de flujo con lápiz y papel pero también hay aplicaciones interesante para hacer diagramas de flujo. Una de ellas es Diagrams. Esta aplicación gratuita y de código abierto ayuda a crear una gran variedad de diagramas en Windows, Linux y macOS, agregando imágenes, configurando los textos y eligiendo el tipo de fuente, etc. El alumnado tendrá la opción de diseñar diagramas de flujo, mapas mentales…. y otro tipo de representaciones aunque para este curso con las que hemos nombrado tenemos suficiente. Su interfaz es muy práctica e intuitiva e incorpora capas que facilitan la edición. Otra opción es Mindomo. En este caso no hablamos de software libre. Se trata de un software colaborativo en línea para realizar diagramas de flujo, mapas mentales… y otras muchas cosas… aunque para este curso estas nos parecen las más adecuadas. Software Freemium ofrece sus servicios básicos de forma gratuita, si bien se cobra por las funciones prémium. La versión gratuita tiene un límite de tres mapas mentales y funciones prémium inhabilitadas, como carga de audio/video, descarga de PDF, PowerPoint y Excel y protección con contraseña. El software se puede usar desde cualquier navegador web estándar o instalando la aplicación gratuita para escritorio, iPad y Android.