Dibujar objetos geométricos con el editor gráfico

Puntos, rectas (paralelas, perpendiculares, bisectrices, mediatrices...), semirrectas, circunferencias (a partir de centro y radio, a partir de 3 puntos dados...), polígonos regulares…

En este video se explican algunas cuestiones básicas sobre el funcionamiento de GeoGebra que hay que tener muy en cuenta. 

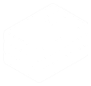
Añadiremos dos cuestiones más. Todas las herramientas son muy intuitivas de usar y cada objeto que crean tiene un conjunto de propiedades que se pueden modificar en la configuración como hemos visto en el video. Además, podemos seleccionar que herramientas se pueden visualizar principalmente si queremos que el alumnado trabaje con una aplicación que hayamos hecho. Para ello iremos al menú “Herramientas”(en las tres líneas horizontales en la parte superior derecha de la ventana de la aplicación) y clicamos en “Personalizar la barra de herramientas”

Fig. 2-1 Personalizar la barra de herramientas

Podemos desplazar con el ratón las herramientas de un lado a otro. A la derecha están las ocultas y a la izquierda las visibles. Hay una barra de herramientas para cada Vista del GeoGebra. La podemos seleccionar en la parte superior derecha de la ventana.

Por otra parte, veréis que el programa dispone de un teclado propio que aparece cuando vamos a escribir en la línea de Entrada. Dispone de varios tipos de símbolos y caracteres que podéis ir viendo, clicando en cada una de las pestañas que están a disposición del usuario. No siempre es fácil encontrar el símbolo que nos interesa.

Fig. 2-2 Teclados del programa

Veamos una construcción muy completa: cómo construir el arco capaz, el lugar geométrico de los puntos del plano desde los cuales se ven los extremos de un segmento desde un mismo ángulo. Para ello construiremos un segmento en cualquier lugar de la Vista Gráfica. GeoGebra asignará a los extremos del segmento las etiquetas A y B (si no hay ninguna construcción anterior).

• Creamos un deslizador con la herramienta 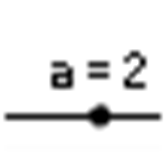   clicando en el lugar que más nos convenga de la Vista Gráfica. Escogemos la variante “Ángulo” y ponemos como incremento 1º. Cómo hemos dicho es mejor no borrar el símbolo de grados porque es propio del programa y no sirve el del teclado del ordenador. El ángulo por defecto es de 45º.
• Con la herramienta “Ángulo dada su amplitud” clicamos en B y luego en A y cómo ángulo introducimos el nombre del deslizador (probablemente a). Aparecerá un punto B’.
• Con la herramienta Semirrecta clicamos en A y B-
• Dibujamos la mediatriz del segmento AB clicando en el mismo con la herramienta “Mediatriz”
• Hallamos la perpendicular a la semirrecta AB’ que pasa por A con la herramienta “Recta perpendicular”
• Hallamos la intersección de dicha recta con la mediatriz de AB con la herramienta  “Intersección” . Obtenemos el punto 
• Usamos la herramienta “Arco de circunferencia” clicando en C y luego en A y en B.
• Con la herramienta “Punto” clicamos sobre el arco y aparece un punto D que se mueve por el mismo.
• Calculamos el ángulo que forman A, D y B con la herramienta “Ángulo” 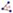. Obtenemos el valor del deslizador si hemos dibujado bien el arco. En caso contrario habrá que volver a construirlo clicando primero en B y luego en A. 

Varias cuestiones que destacar sobre esta construcción:

1. Obsérvese que el nombre de las herramientas se corresponde con la acción que realizan sin confusión posible. La explicación parece repetitiva y redundante, pero vale la pena destacar este hecho. La ventaja de GeoGebra es que añade dinamismo a la construcción.
2. Para alguna construcción nos podemos encontrar con sorpresas si no tenemos en cuenta el sentido horario u antihorario. GeoGebra prioriza el sentido antihorario, aunque también nos ofrece la posibilidad de elegir. Iremos viendo ejemplos, aunque la solución sencilla cuando algo no sale bien es clicar en el botón de “Deshacer” que está al lado de la lupa en la parte superior derecha. 
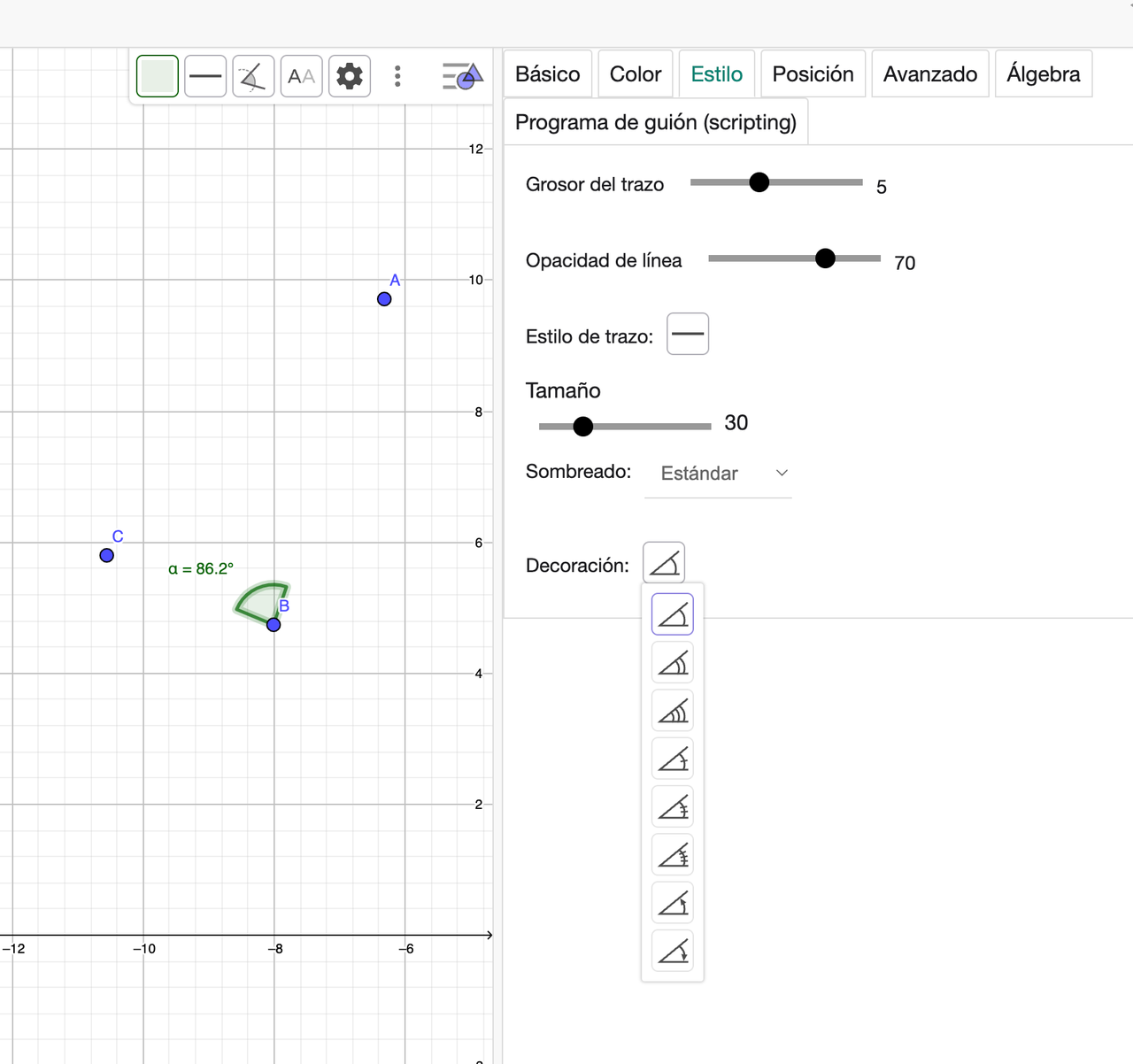
3. La pestaña “Estilo” de la configuración de un ángulo nos ofrece muchas posibilidades: grosor del trazo, estilo de trazo, tamaño, sombreado (¡que podría ser una imagen!) y decoración. En el caso de la decoración podemos definir también las características de esta (por ejemplo, ángulo y espaciado como puede verse en la figura). Pueden parecer excesivas tantas opciones, pero los programadores quieren poner a disposición del usuario todo lo imaginable y más para facilitar su trabajo (aunque a veces complican el uso del programa).

Fig. 2-3a Opciones disponibles en la configuración de un ángulo

Fig. 2-3b Opciones disponibles en la configuración de un ángulo

Aprovecharemos esta construcción del arco capaz para explicar un ejemplo de cómo podemos construir nuestras propias herramientas.

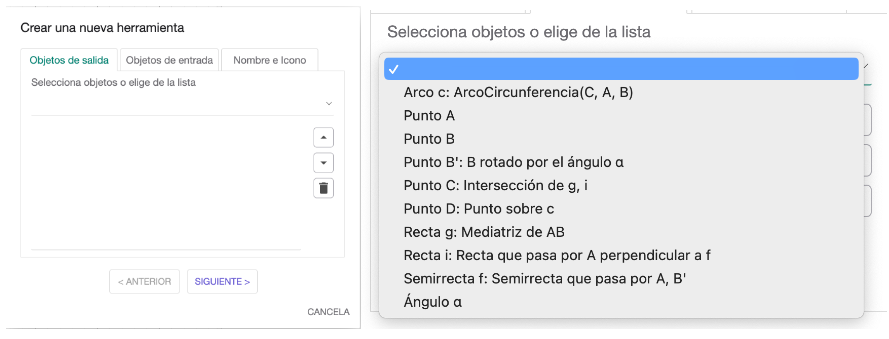
Una vez acabada la construcción del arco capaz vamos de nuevo al menú “Herramientas” y clicamos en “Crear una nueva herramienta”. Aparece una ventana emergente con tres pestañas. En la segunda introducimos los Objetos de entrada. Usando la lista desplegable clicamos, sucesivamente, en A, en B y en Ángulo (el deslizador). En la primera pestaña, como Objetos de salida, clicamos en el Arco de circunferencia. En la tercera pestaña ponemos un nombre (GeoGebra asignará un nombre a la herramienta a partir de este) y, como ayuda, “Dos puntos y un ángulo”. Una vez concluido el proceso tendremos la nueva herramienta.

Fig. 2-4 Ventana para la creación de una nueva herramienta

Podemos probarla con la construcción de un triángulo dados un lado, un ángulo adyacente y el ángulo opuesto al mismo.