Lugares geométricos

Los problemas de optimización son un muy buen ejemplo del uso de la herramienta del Lugar geométrico  con la que ya hemos visto algunos ejemplos. Vamos a ver otro con un problema de geometría 3D del profesor Ricard Peiró Estruch, autor del calendario matemático de la SEMCV.

Consideremos un tetraedro regular ABCD. Sea E un punto de la arista AB. Determinar el valor máximo del ángulo ÐCED cuando E recorre la arista AB.

Tenemos abiertas tres Vistas: Álgebra, Gráfica y Gráficas 3D y expresamos los ángulos en radianes.

• Construimos un tetraedro regular a partir de dos puntos A y B. C y D son los otros dos puntos del tetraedro.
• Creamos un punto E en la arista AB. Escribimos d=AE en la Entrada.
• Escribimos t=Ángulo(C,E,D) en la Entrada de la Vista algebraica.
• Escribimos P=(d,t). Aparecerá un punto en la Vista Gráfica (hay que indicarlo para que no salga también en la Vista 3D). Si es necesario ajustamos los ejes para visualizarlo. Activamos su rastro.
• Animamos el punto E y observamos la curva que describe el punto P.
• Clicamos en la herramienta del lugar geométrico y, seguidamente, clicamos en P y en E. La curva tarda un poco en aparecer, seguramente por el cálculo que tiene que hacer el programa. Hacemos que solo se vea en la Vista Gráfica.

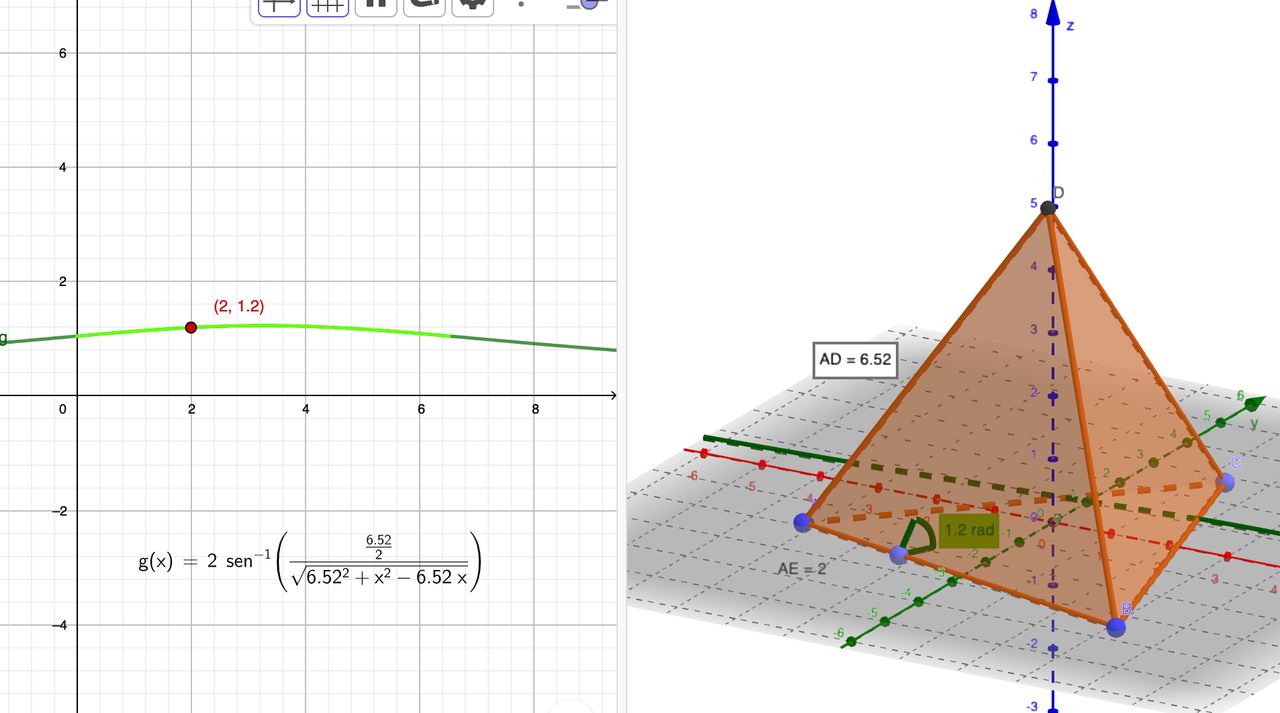
La función no es trivial. Se puede demostrar geométricamente con relativa facilidad que el máximo corresponde al punto medio de AB pero, analíticamente, la expresión es la que aparece en la figura (y la gráfica coincide con la que da el programa).

Fig. 6-2 Solución del problema de optimización