Sistemas de ecuaciones lineales 3x3. Matrices y determinantes.

Podemos resolver gráficamente sistemas de ecuaciones lineales con tres incógnitas escribiendo directamente las ecuaciones en la Vista algebraica, incluso con parámetros. Las rectas que resultan de las intersecciones de los planos con la herramienta  nos darán la solución del sistema si la hay. Usaremos la herramienta de intersección  con dos de las rectas obtenidas para hallarla.

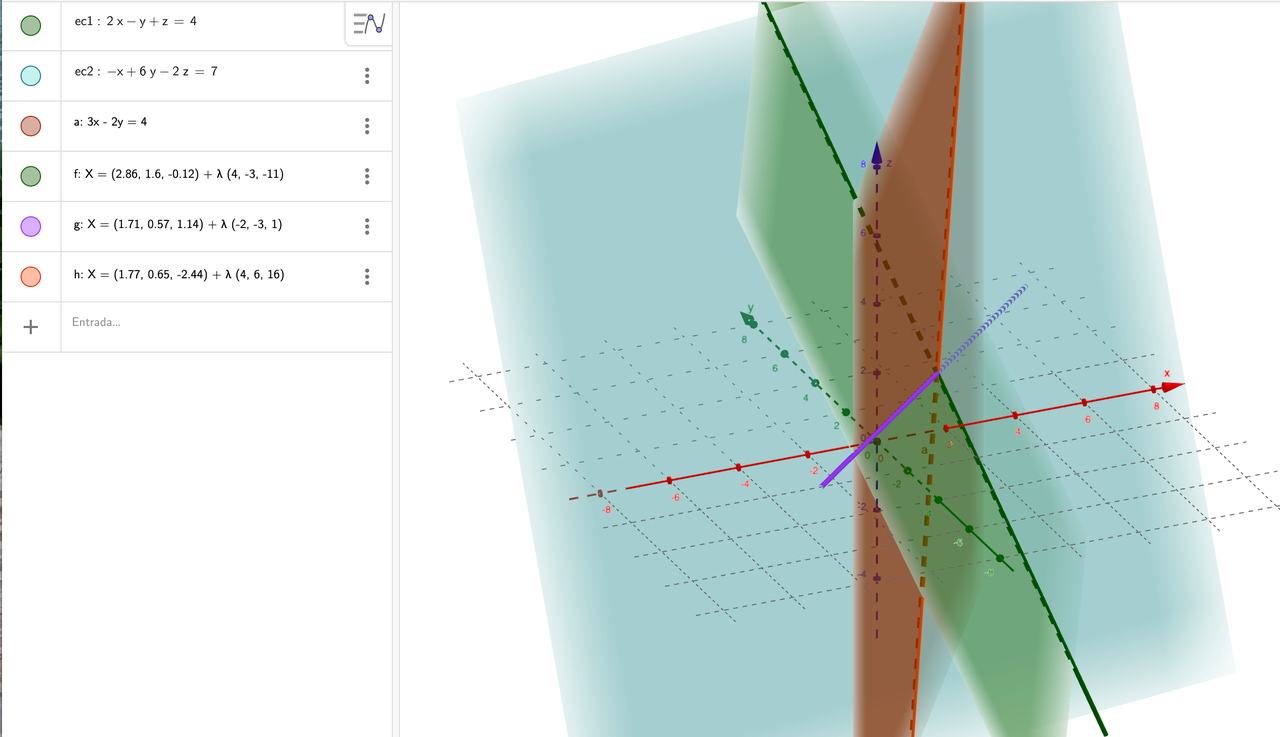
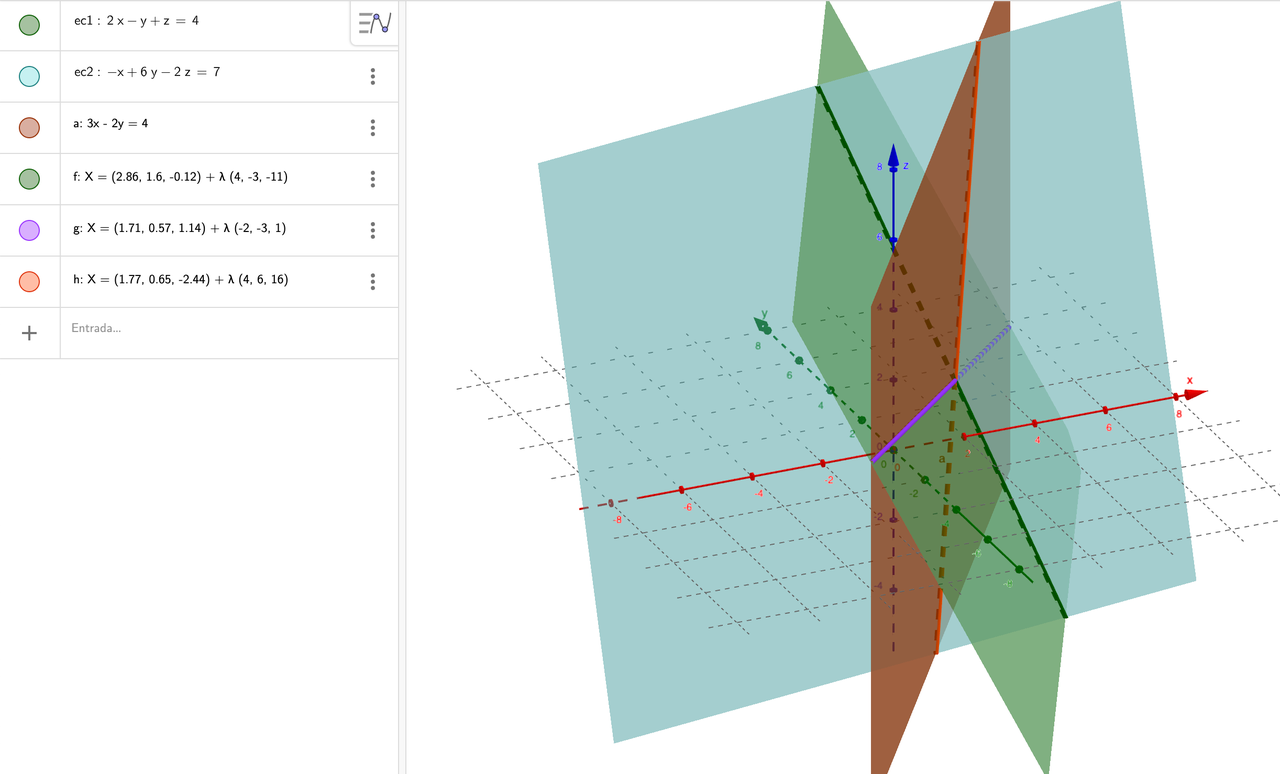
Hay un inconveniente al escribir una ecuación sin término en z. Es conveniente añadir +0 z porque sino el programa la interpreta como una función de dos variables. Se pueden hallar igualmente las intersecciones, pero mejor si se puede evitar. Si el plano nos aparece con cuadrícula habrá que poner a 0 el Grosor del trazo en las opciones de configuración de este.

Fig 5-5 Intersección de 3 planos para la resolución de un sistema de ecuaciones

Fig. 5-6 Uso del recorte en las opciones de la Vista Gráficas 3D

Fig. 5-7 Opciones de grosor de trazo y trazo oculto

Para introducir matrices con GeoGebra y operar con ellas tenemos dos procedimientos que explicamos en este video.

Para resolver sistemas de ecuaciones de n ecuaciones con n incógnitas bastará introducir la matriz de coeficientes como hemos explicado y el vector o la matriz (si son más de tres ecuaciones) con los términos independientes. El resultado será la matriz inversa de la matriz de coeficientes aplicada a este vector o matriz. Mejor introducir los parámetros (de haberlos) al principio y no después de introducir las matrices.

Y puestos a probar…

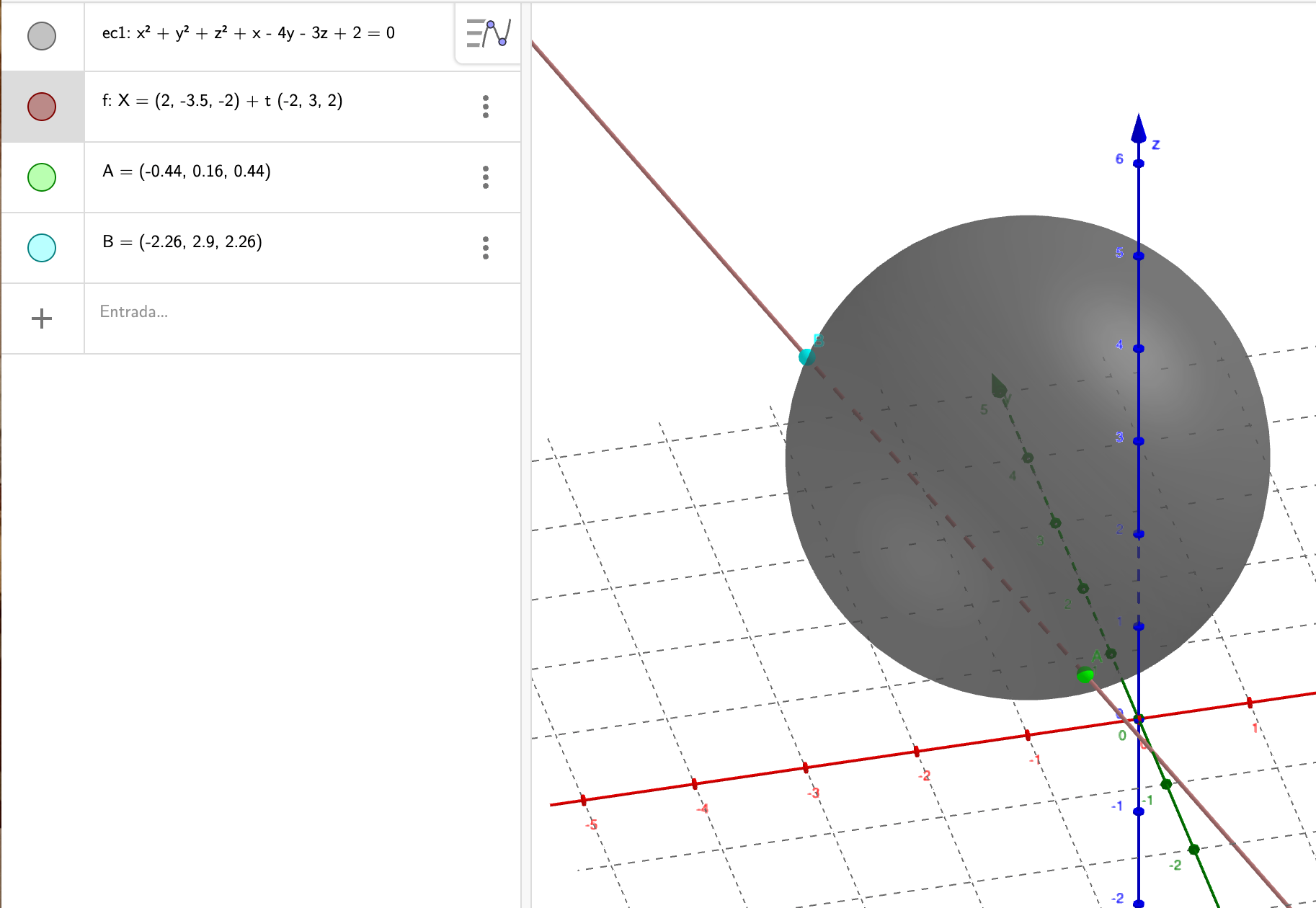
Fig. 5-8 Intersección de una recta y una esfera

La recta y la esfera se han introducido con las ecuaciones que se ven en la figura (en el caso de la recta no es necesario escribir X=).