Geometría del triángulo: puntos notables y teorema de Pitágoras

En esta actividad (con cinco aplicaciones) se explica el procedimiento para construir las rectas y los puntos notables del triángulo. Se puede utilizar posteriormente para una actividad de GeoGebra Classroom que explicaremos en su momento.

En la última aplicación se utiliza una “Casilla de control” que permite mostrar o no los objetos que elijamos. Al clicar en el icono y luego en donde queramos de la Vista Gráfica aparece una ventana emergente. En el Rótulo escribimos el texto con una referencia a los objetos que se quieren mostrar o no y una lista con los objetos de la aplicación para indicar aquellos cuya visibilidad queremos controlar (que también podemos señalar en la Vista Gráfica). Cada casilla se corresponde con una variable booleana (que saldrá en la línea de Entrada como true o false)

Es posible que algunos objetos dependan de más de una condición. Este caso es más complejo y hay que recurrir a operadores lógicos. Supongamos un objeto cuya visibilidad viene condicionada por dos casillas de control de nombres a y b. Queremos mostrarlo si se cumple a pero no b. Iremos a la configuración del objeto (la ruedecita) y en la pestaña “Avanzado” aparece “Condición para mostrar el objeto”. Allí escribiremos: a∧(¬b) con el teclado del programa.

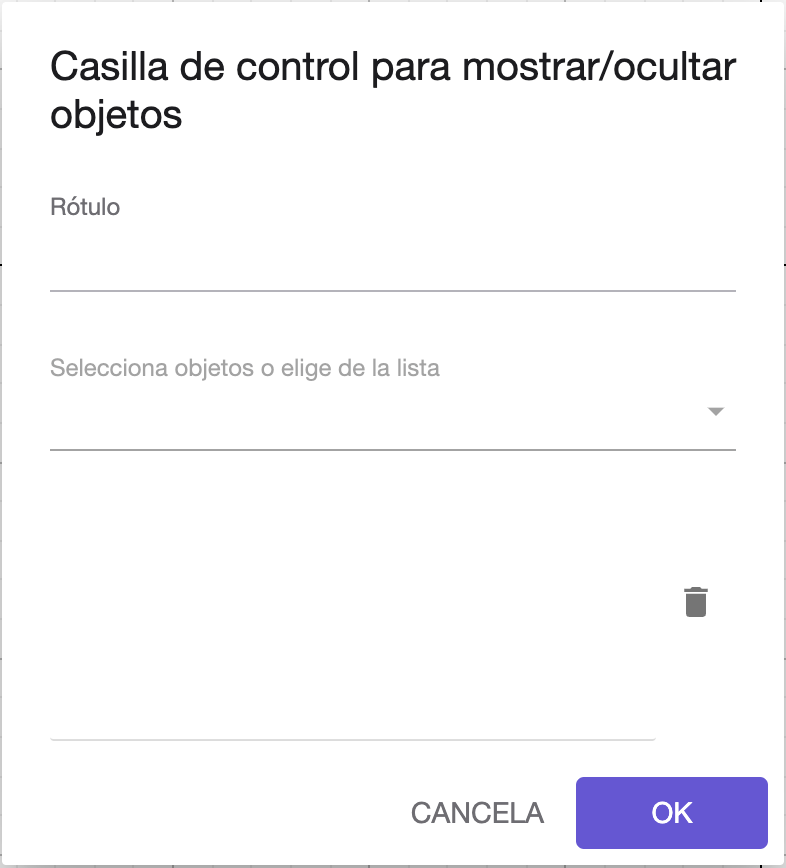 Fig. 2-6a Diálogo para casilla de control

Fig. 2-6b Teclado de símbolos

Existe una cantidad ingente de aplicaciones con GeoGebra sobre el teorema de Pitágoras. Aquí nos limitaremos a hacer una construcción muy sencilla para introducir la herramienta “Texto” de GeoGebra. Obviaremos indicar las herramientas que ya hemos introducido.

• Dibujamos un segmento AB (arbitrario).
• Construimos la perpendicular al segmento que pasa por B.
• Sobre esta perpendicular dibujamos un punto C.
• Dibujamos el polígono ABC. Ya tenemos el triángulo rectángulo.
• Dibujaremos un cuadrado sobre cada uno de los lados. Para ello usaremos la herramienta del polígono regular introduciendo 4 como número de lados. Si vemos que el cuadrado aparece dentro del triángulo deshacemos la acción y la repetimos invirtiendo el orden de los vértices. Como sugerencia podemos colorear los cuadrados.
• Sugerimos dibujar otros polígonos regulares sobre cada uno de los lados y ver que sucede con las áreas de estos polígonos. 

La herramienta para escribir texto de GeoGebra es muy potente y genera textos dinámicos que cambian si se modifica algún parámetro del texto. La ventana emergente nos da la posibilidad de escribir texto sin más pero también podemos introducir objetos de la construcción e incluso fórmulas. Lo podemos ver en el siguiente vídeo.