MONTAJE 3 Timbre
Enunciado
Queremos que hagas un programa en el Echidna que si se pulsa SL que suene el buzzer y si pulso SL que suene un tono
Ojo, sube el volumen, girando el potenciómetro hacia la derecha
Lo puedes oir o por el buzzer o por el jack de audio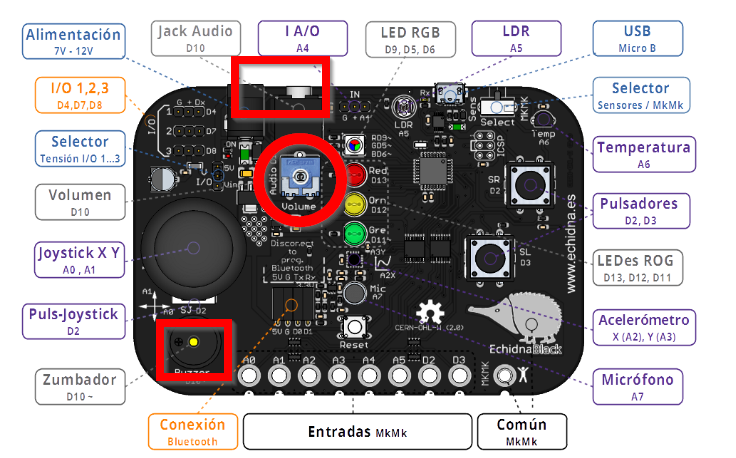
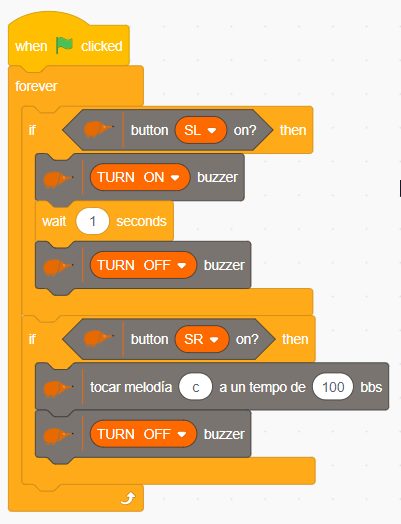
Solución con EchidnaScratch
El programa lo tienes en el repositorio https://github.com/JavierQuintana/Echidna
Esta es la equivalencia entre notas y la nomenclatura Midi :
| NOTA | MIDI |
| A | LA |
| B | SI |
| C | DO |
| D | RE |
| E | MI |
| F | FA |
| G | SOL |
Solución con mBlock
Con mBlock no tiene instrucciones específicas para Echidna luego inventaremos un poco los tonos
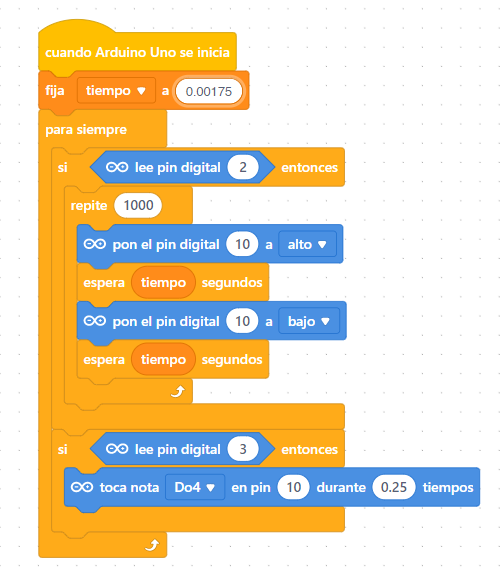
- Cuando se pulsa D2 suene una onda cuadrada de 282Hz o sea una duración 0.035 segundos (0.0175seg el bajo y 0.0175seg el alto).
- Si se pulsa el botón D3 que suene el tono C4 que es aproximadamente esa frecuencia.
El programa lo tienes aquí https://planet.mblock.cc/project/3228713
OJO no se puede hacer "en vivo" hay que cargarlo en el ordenador. La instrucción toca nota no permite utilizar Arduino en vivo
OJO sube el volumen del potenciómetro
El resultado es este vídeo:
Si pulsamos D2 el sonido es más agudo que pulsando D3 que corresponde a la nota C4 ¿Por qué? Porque la señal es cuadrada.
BrainFad = pedo mental
Bueno una explicación más rigurosa de por qué la señal es más aguda con señales cuadras es lo siguiente:
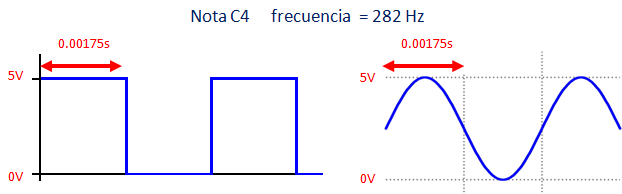
Los cálculos del tiempo de subida y bajada tiempo=0.00175s calculados anteriormente están bien hechos ¿por qué no reproduce bien el tono de la nota C4? por esto:
No es lo mismo una onda analógica sinusoidal de 282 Hz que una onda digital cuadrada que es lo que se reproduce en la salida digital D10
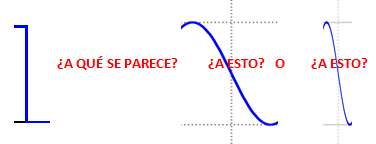
¿Y por qué se oye más agudo? Vamos a fijarnos en una transición por ejemplo la de bajada de 5V a 0V ¿A qué se parece más esa transición?
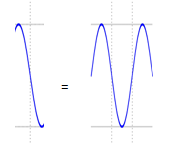
Evidentemente a la segunda, y esa pendiente tan vertical corresponde más a ondas agudas:
Por lo tanto se oye más agudo, por eso es.
Ya sé que el anterior razonamiento, si lo lee algún físico, le producirá un rechinar de dientes, así que para ellos la explicación formal es que una onda cuadrada, según la transformada de Fourier, reproduce armónicos de orden superior, incluso infinitos si fuese perfecta.
via GIPHY
No comments to display
No comments to display